亮点文章
摘要 +
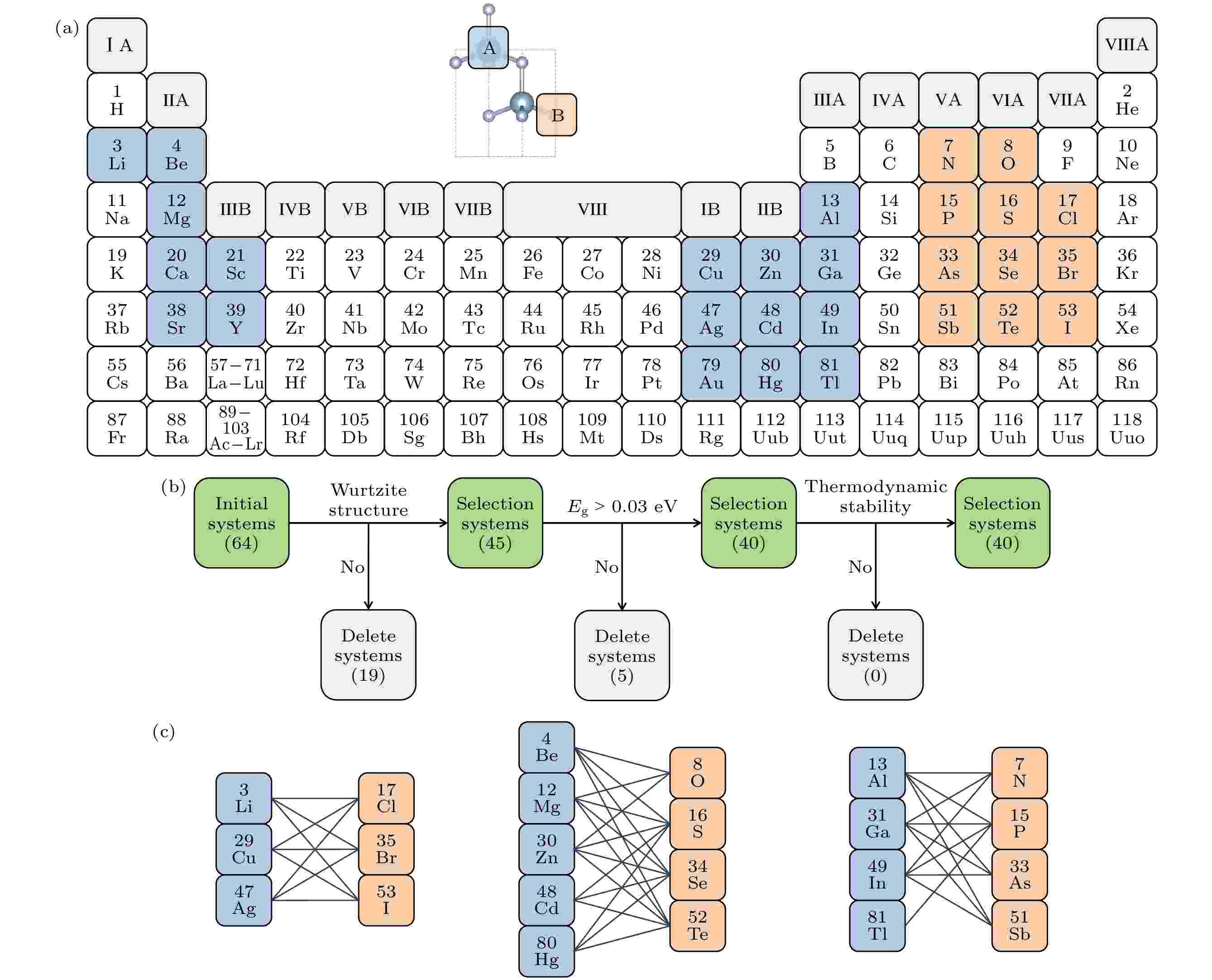
自发极化强度是衡量铁电材料极化能力的关键指标. 新兴的纤锌矿铁电材料因较高的自发极化而受到广泛关注, 但目前对影响这一性质的关键因素的理解仍然不足. 本文旨在通过结合机器学习和第一性原理方法来解决这一问题. 首先, 计算了40种二元和89种简单三元纤锌矿材料的自发极化强度, 并从元素基本属性、晶体结构参数和电子性质中提取了多种特征. 随后, 采用Boruta算法和距离相关系数分析方法进行特征筛选, 提出了一个全面而精确的纤锌矿材料自发极化强度的机器学习预测模型. 进一步借助SHapley Additive exPlanations分析方法, 阐明了影响自发极化强度的关键因素是阳离子离子势的均值IPi_Aave和晶胞参数a等. 本研究弥补了目前对自发极化强度多因素的影响机制理解的缺乏, 为系统评估新兴纤锌矿材料的自发极化强度提供了帮助, 有助于加快性能优异的纤锌矿铁电材料的筛选. 本文数据集可在https://www.doi.org/10.57760/sciencedb.j00213.00073 中访问获取.
摘要 +
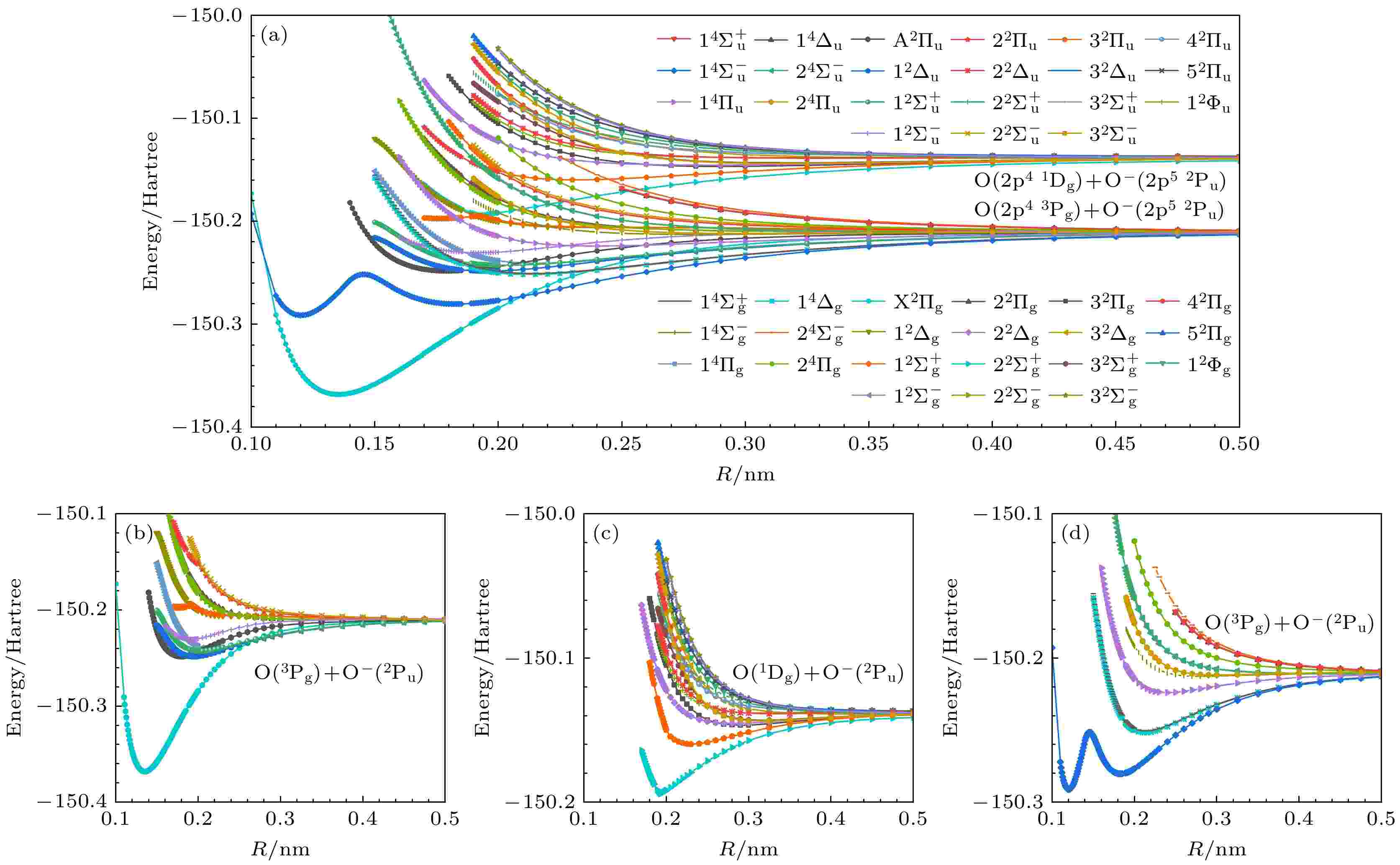
本文采用完全活性空间自洽场(complete active space self-consistent field, CASSCF)和加戴维森校正的多参考组态相互作用(multireference configuration interaction with Davidson correction, MRCI+Q)方法, 研究了超氧阴离子(${\text{O}}_{2}^{{ - }}$)的低激发电子态及自旋-轨道耦合(spin-orbit coupling, SOC)效应对电子态的影响. 使用aug-cc-pV5Z-dk基组, 计算了${\text{O}}_{2}^{{ - }}$第一和第二解离极限对应的42个Λ-S态的势能曲线(potential energy curves, PECs)以及束缚态的光谱常数. 同时考虑SOC效应, 计算了这42个Λ-S态分裂形成的84个Ω态的PECs和部分束缚态的光谱常数. 其中第一解离极限结果与已有文献高度一致, 第二解离极限结果为本文计算提供. 这些结果为研究${\text{O}}_{2}^{{ - }}$的电子结构和光谱性质提供了重要的理论依据. 针对${{\text{a}}^{4}}{{\Sigma }}_{\text{u}}^{{ - }}$态的双势阱现象, 本文通过比较不同基组下的计算结果, 证实了${{\text{a}}^{4}}{{\Sigma }}_{\text{u}}^{{ - }}$态的双势阱形成源于与${{2}^{4}}{{\Sigma }}_{\text{u}}^{{ - }}$态的避免交叉影响. 此外, 研究发现基组大小直接影响${{\text{a}}^{4}}{{\Sigma }}_{\text{u}}^{{ - }}$态的首个势阱深度, 这进一步表明基组选择对光谱常数计算的精确性至关重要. 本文数据集可在科学数据银行https://doi.org/10.57760/sciencedb.j00213.00076 中访问获取.
摘要 +
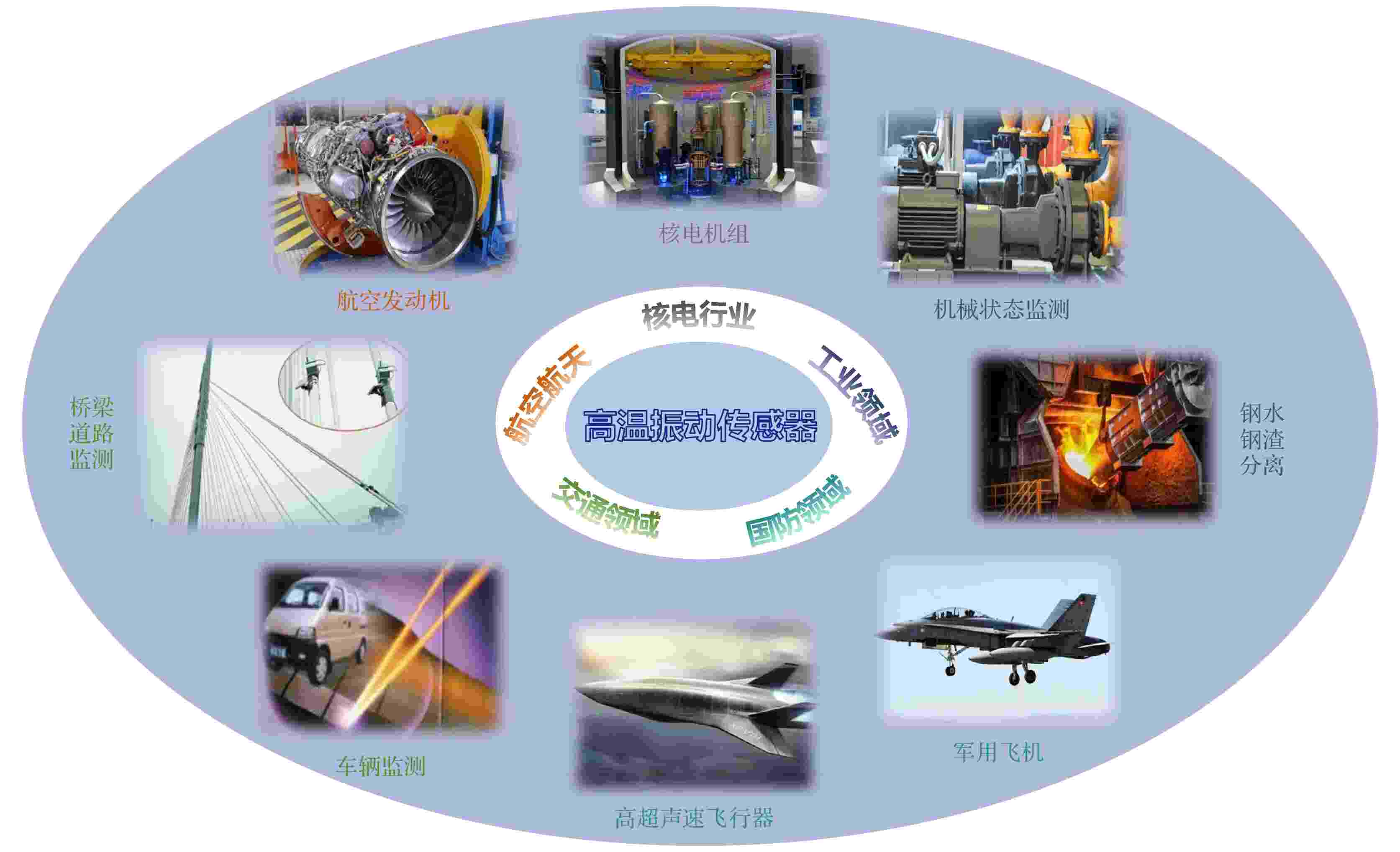
压电振动传感器与其他振动传感技术相比具有频率范围宽、动态范围大、结构简单、工作可靠、体积小等优点, 在核电行业、航空航天、轨道交通及国防军工等多个领域有着广泛的应用. 然而, 随着振动测试技术的飞速发展以及应用领域的不断拓宽, 对压电振动传感器在极端环境中长时服役的可靠性提出了更高要求, 如何提高压电振动传感器的服役温度满足极端环境下的应用需求是目前迫切解决的问题. 本文综述了高温压电传感技术应用场景和工作原理, 讨论了常见的高温压电陶瓷和晶体材料, 系统地总结了现有的压电振动传感器工作模式、不同类型压电振动传感器结构及传感器振动校准装置, 重点介绍了近年来国内外高温振动传感器的研究进展. 在此基础上, 探讨了高温压电振动传感器当前面临的问题及未来发展趋势, 为开发下一代极端环境应用的超高温振动传感器提供了思路, 有望促进国内高温压电振动传感技术的进一步研究.
摘要 +
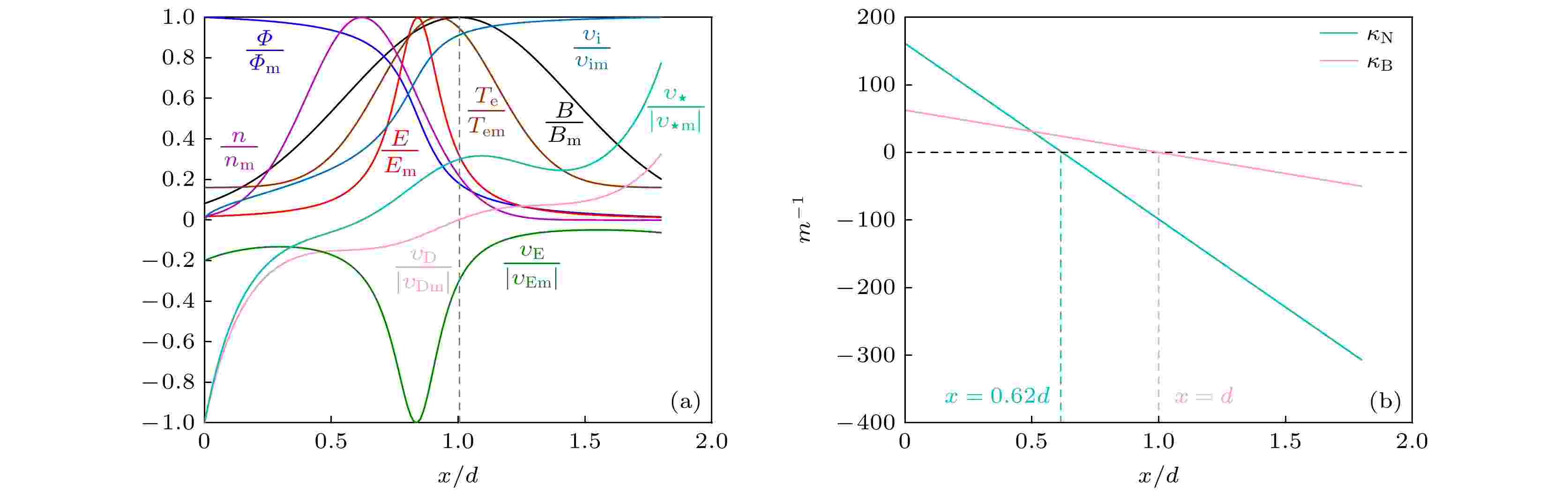
在霍尔推力器中, 电子漂移、电子碰撞, 以及等离子体密度、温度、磁场梯度所蕴含的自由能会驱动各种频率和波长的不稳定性. 不稳定性的存在会破坏等离子体的稳定放电, 削弱推力器与电源处理单元的匹配度, 降低推力器的性能. 基于此, 本文利用基于流体模型推导的色散关系研究了霍尔推力器中由电子碰撞、等离子体密度和磁场梯度驱动的不稳定性. 结果表明: 1)在考虑电子惯性、电子与中性原子的碰撞, 以及电子${\boldsymbol{E}} \times {\boldsymbol{B}}$漂移时能够在推力器近阳极区到羽流区内的任一轴向位置处激发不稳定性. 随着角向波数${k_y}$的增大($k = 2{\text{π /}}\lambda $, $\lambda $为波长), 模式将从由碰撞激发的低杂波不稳定性转变为离子声波不稳定性. 当${k_y} = 10 {{\text{ m}}^{ - 1}}$时, 最大增长率${\gamma _{\max }}$对应频率${\omega _{\text{r}}}$随着碰撞频率${\nu _{{\text{en}}}}$的增大而轻微减小; 当$ {k_y} = 300 {{\text{ m}}^{ - 1}} $时, ${\gamma _{\max }}$对应的频率${\omega _{\text{r}}}$以及最大频率${\omega _{{\text{rmax}}}}$几乎不随碰撞频率变化. 不依赖于$ {k_y} $的大小, 对于碰撞激发的不稳定性, 模式的增长率随着碰撞频率的增大而增大. 同时考虑电子惯性、电子碰撞效应, 以及密度梯度时, 密度梯度对驱动不稳定性占主导作用. 模式的动力学行为不会随${k_y}$的增大而变化, 但模式的本征值随${k_y}$的增大而增大. 在密度梯度${\kappa _{\text{N}}} = 0$的两侧, 由于密度梯度引起的抗磁性漂移频率${\omega _{\text{s}}}$的符号发生了变化, 模式的本征值在${\kappa _{\text{N}}} = 0$两侧有相反的变化趋势: 当${\omega _*}$与${\omega _{\text{r}}}$符号相反时, 密度梯度对不稳定性的激发有削弱作用(${\kappa _{\text{N}}} \gt 0$); 当${\omega _*}$与${\omega _{\text{r}}}$符号相同时, 密度梯度对不稳定性的激发有增强作用(${\kappa _{\text{N}}} \lt 0$); 3)在模型中同时考虑等离子体密度梯度、磁场梯度, 以及电子惯性和碰撞效应时, 模式本征值的变化依赖于电子的漂移频率, 以及密度和磁场梯度引起的抗磁性漂移频率的相对大小. 当仅包含密度梯度和磁场梯度时, 推力器放电通道内将出现稳定窗, 即增长率为0的区间; 包含电子惯性和碰撞效应后, 稳定窗消失.

摘要 +
快中子多重性测量技术是军控核查领域一项重要的无损检测技术, 可用于核材料的质量衡算. 但该方法是基于点模型假设建立的, 会造成系统偏差. 为修正偏差提升测量精度, 本文对两种不同形状的样品进行了快中子多重性模拟测量, 得到了材料空间体积内中子产生、吸收和净增长随位置的变化关系, 发现了中子泄漏增殖系数的空间变化规律. 根据中子多重性阶乘矩与待测参数间的函数关系, 提出了一种基于空间增殖系数修正的方法, 通过引入修正因子$ {g_n} $, 推导了快中子多重性加权点模型方程. 为验证该方法的准确性, 本文通过Geant4搭建了一套测量模型, 对球体和圆柱体两种形状的公斤级钚样品进行了模拟测量. 结果表明, 快中子多重性加权点模型方程的测量精度高于点模型方程, 测量偏差缩小至6%以内, 提供了一种求解公斤级钚样品质量的优化方法, 推动了快中子多重性测量技术向前发展.
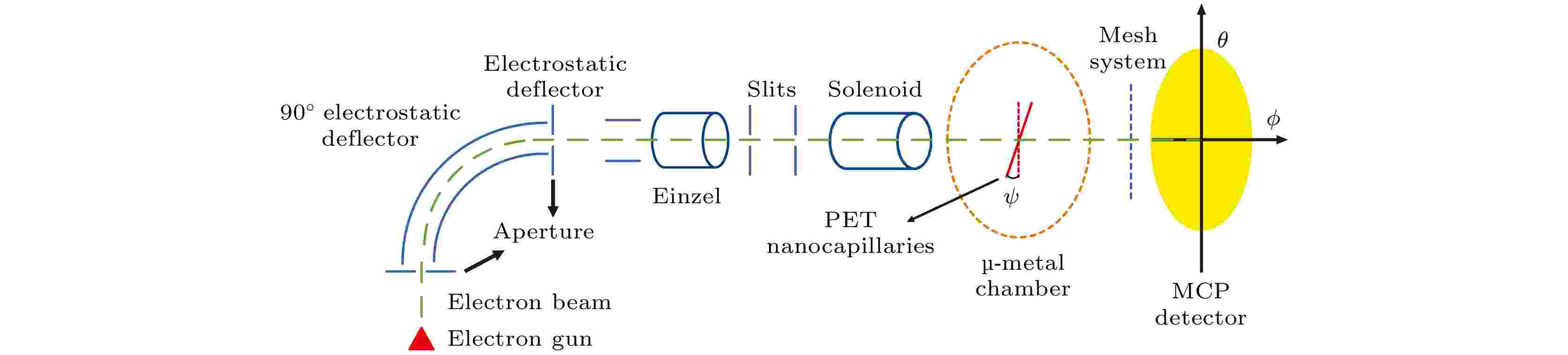
摘要 +
研究了2 keV电子在直径为800 nm, 长度为10 μm的聚对苯二甲酸乙二醇酯(polyethylene terephthalate, PET)纳米通道中的输运过程. 结果表明, 当纳米微通道倾角为0°时, 穿透电子的穿透率可达10%, 而当倾角大于几何张角时, 穿透电子的透射率小于1%. 穿透电子角分布中心没有随微孔倾角的变化而移动, 因此没有如在正离子的情况下那样观察到绝缘微孔对电子的导向效应. 在充电达到稳态时, 当微孔倾角小于几何张角时, 电子分裂成上下两个电子斑. 穿透电子的全角分布的时间演化表明, 在充电开始时, 穿透电子为单电子斑. 随着入射电荷量(充电时间)的累积, 穿透电子被上下拉伸, 并逐渐分裂成两个电子斑. 当纳米微孔的倾角超过几何张角时, 穿透电子的分裂趋于消失. 对电子造成微孔内壁上的电荷沉积的模拟计算表明, 微孔表面被激发出大量空穴, 形成正电荷累积; 而部分入射电子沉积于表面以下更深处, 形成负电荷层, 因此不利于产生类似正离子的导向效应. 本文还讨论了造成穿透电子角分布上下分裂的可能原因, 并据此提出验证电子和离子充电机制不同的新的实验方法. 研究结果为利用绝缘微通道控制电子传输技术的发展提供了支撑.
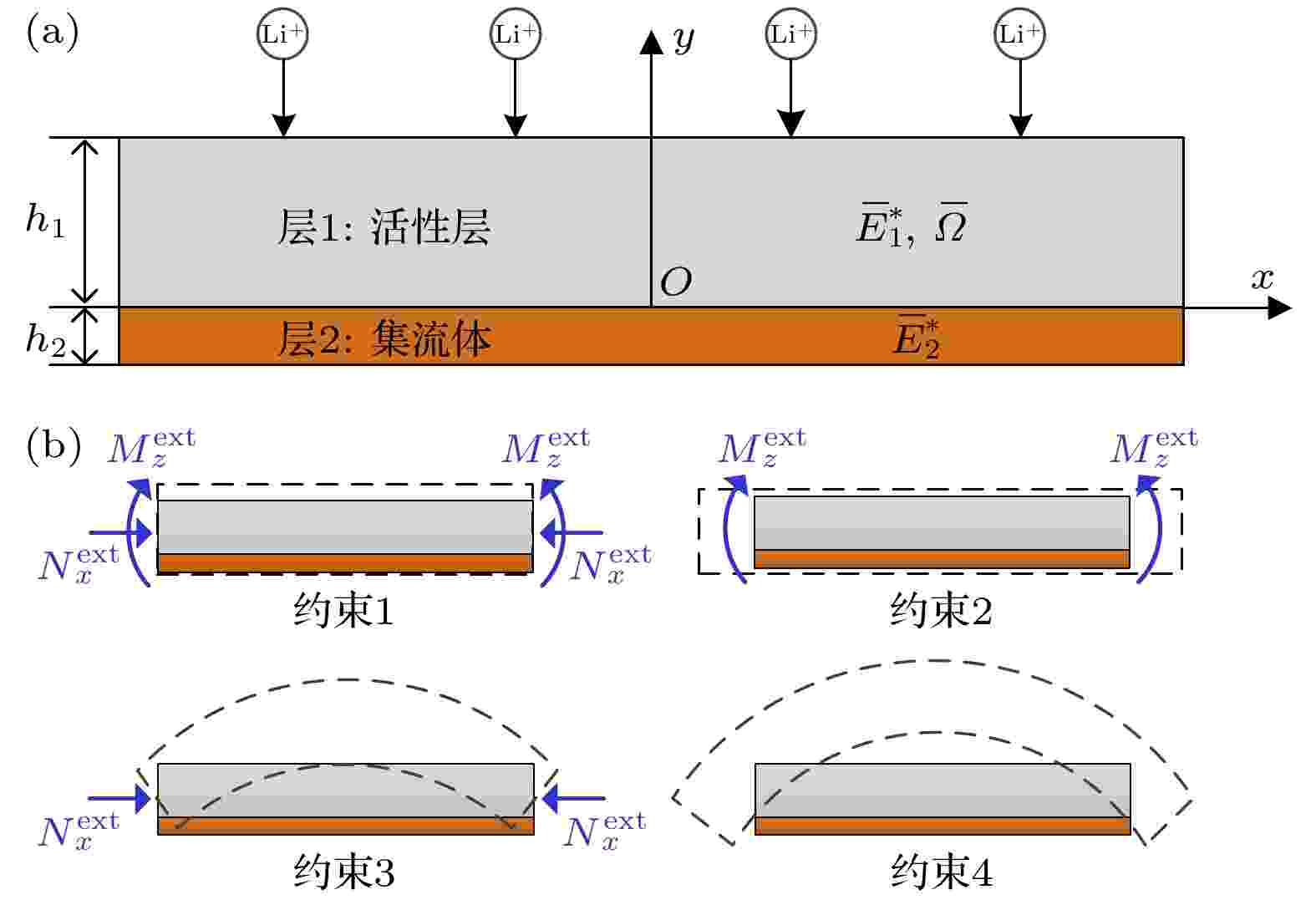
摘要 +
锂离子电池中的电极总是处于特定的约束当中, 这些约束既包括电池内部不可避免的被动结构约束, 又包括一些新兴技术应用场景可能赋予的外部主动约束. 本文主要利用化学-力学双向耦合的基本假设建立描述双层电极结构的理论模型, 考虑4种不同强弱的理想化变形约束作为其边界条件, 并通过数值求解研究在充电过程中这些外部约束对双层电极中Li扩散和应力的影响. 从力学的角度, 所研究的双层电极结构存在侧向伸缩和弯曲变形两个自由度, 弱化的约束条件能够部分或完全激活这些应力释放机制, 从而降低电极结构整体的应力水平, 并提升结构的力学稳定性. 然而, 从电化学的角度, 电极结构的正向弯曲变形所产生的应力梯度会阻碍嵌Li过程, 强化的约束能够部分或完全抑制电极的正向弯曲, 使活性层内Li浓度更加均匀, 从而提高活性层的容量利用率. 这些结果不仅为进一步理解双层电极在更加真实或极端服役条件下的化学-力学响应提供理论参考, 还从设计的角度表明折中的外部约束有利于平衡电极的结构耐久性和电化学性能.
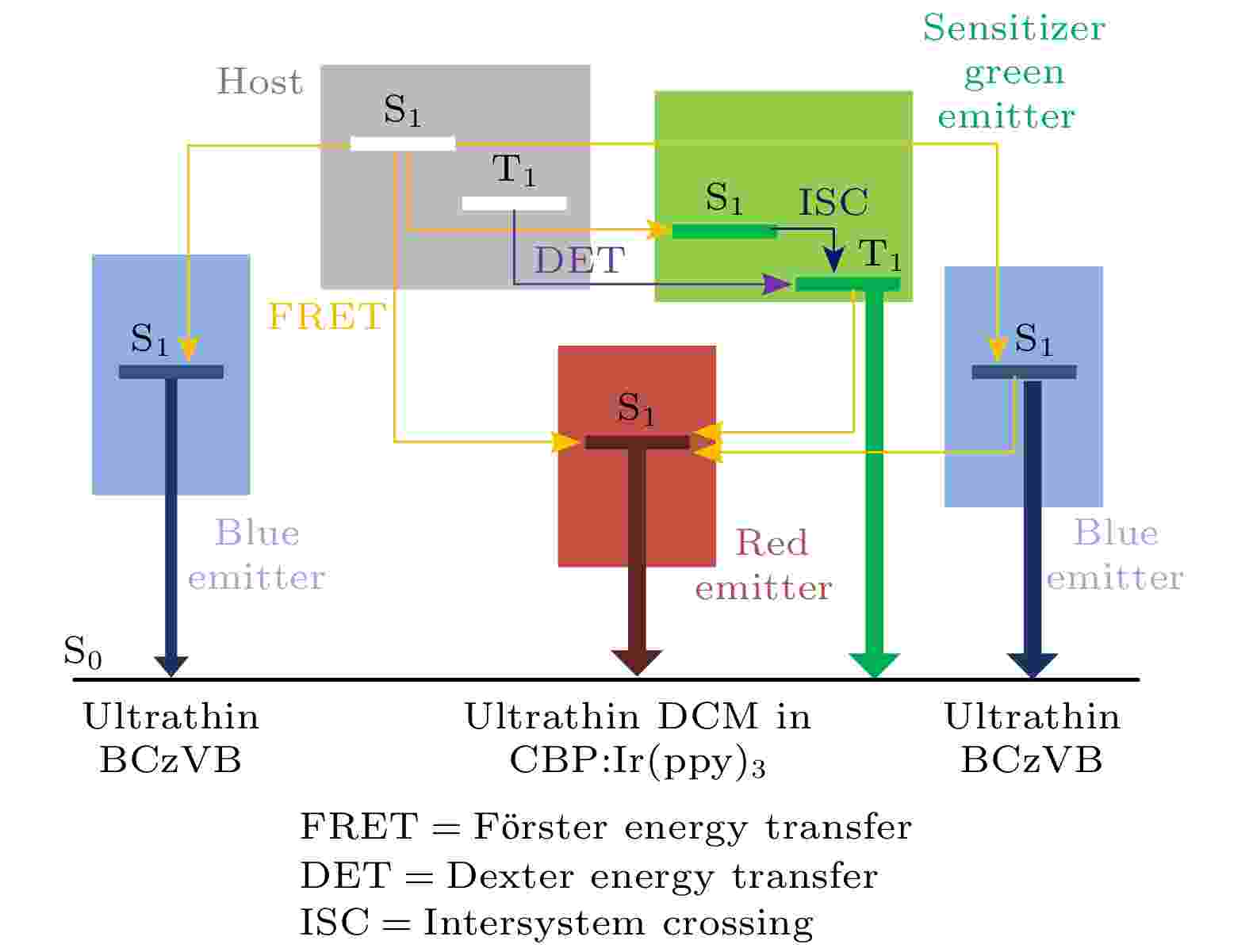
摘要 +
通过超薄层插入与掺杂相结合的方式, 分别以激光染料DCM (4-(Dicyanomethylene) -2-methyl-6-(4-dimethyl-aminostyryl)-4H-pyran)、铱配合物Ir(ppy)3 (tris(2-phenylpyridine) iridium)和联苯乙烯衍生物BCzVB(1, 4-bis[2-(3-N-ethylcarbazoryl)vinyl]benzene)为红色、绿色和蓝色发射体, 制备了磷光敏化荧光白色有机电致发光器件(OLED). 通过改变DCM超薄层在CBP:Ir(ppy)3掺杂层中的插入位置实现了白色发光, 最高外量子效率为2.5%(电流效率为5.1 cd/A), 最高亮度为12400 cd/m2, 且其中一种器件在1 mA/cm2的电流密度下, 国际照明委员会(Commission Internationale de L'Eclairage, CIE)坐标达到了理想白光平衡点(0.33, 0.33). 白光的获得归因于Ir(ppy)3适合的掺杂比例和DCM适合的插入位置, 较好地均衡了红、绿、蓝三基色发光比例. 结果表明, 通过磷光敏化荧光实现三线态激子将部分能量传递给单线态激子, 可望实现高效率白色有机电致发光器件, 从而降低能耗并为促进OLED的应用提供更多空间.
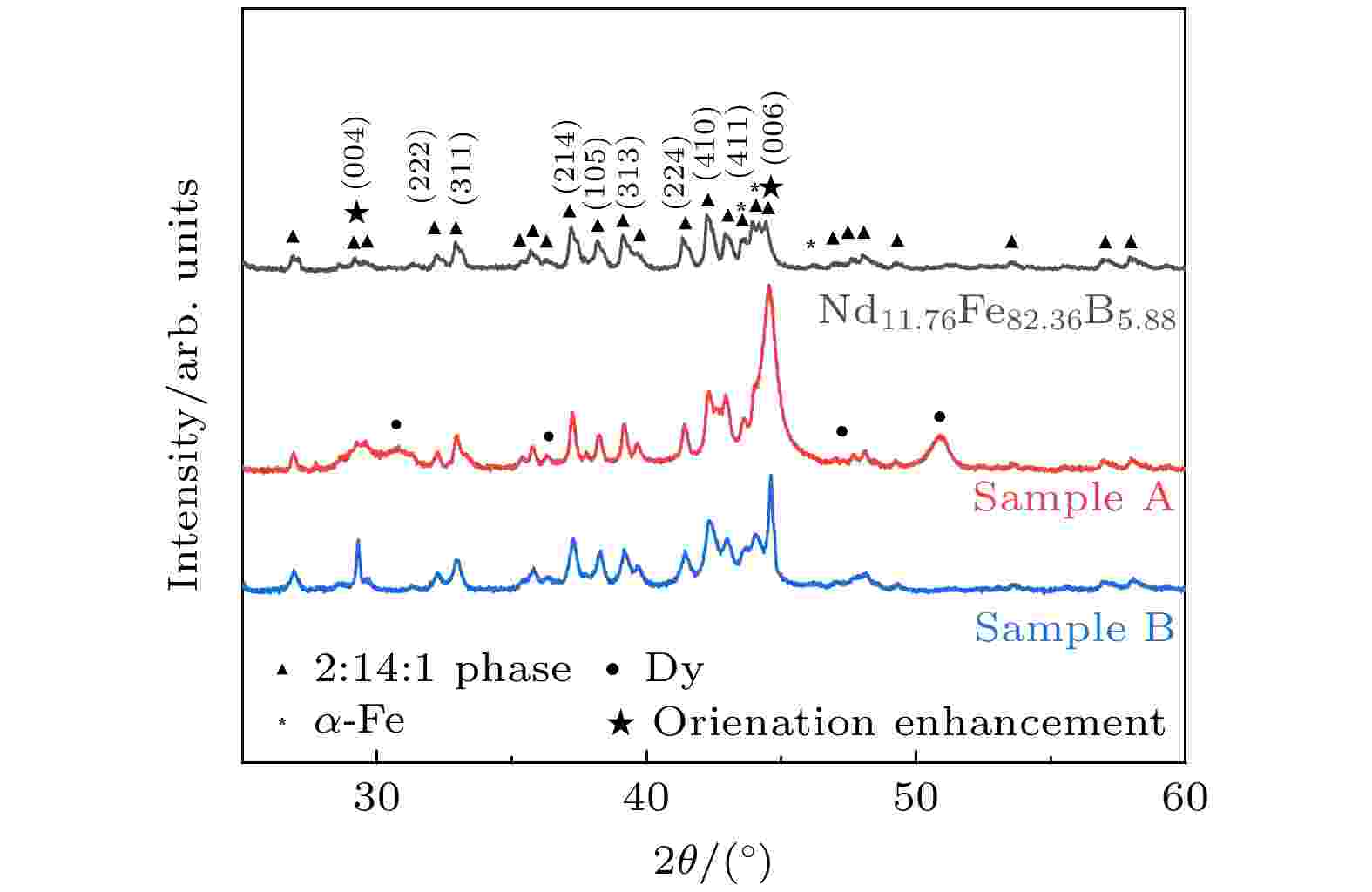
摘要 +
稀土元素具有相似的基态电子性质, 其独特的镧系收缩效应可以降低高熵材料中稀土元素的混合焓, 这对于制备廉价且高性能的高熵稀土金属间化合物至关重要. 本文在分析磁化和反磁化曲线的基础上, 辅以Henkel曲线和磁黏滞系数S计算, 研究了Nd11.76Fe82.36B5.88(NdFeB), 以及高熵稀土永磁合金化合物(La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88和(La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88等快淬条带的反磁化机理. 研究结果发现, 与纯NdFeB相比, 高熵稀土永磁材料的晶间耦合作用显著增强, 而磁偶极相互作用减弱. 这表明, 含重稀土的高熵材料中元素扩散机制在使样品均匀化的同时, 其矫顽力有大幅度提高, 矫顽力机制为硬磁相晶粒中的反磁化畴形核. (La0.2Pr0.2Nd0.2Gd0.2Dy0.2)11.76Fe82.36B5.88的磁黏滞系数大于纯NdFeB, (La0.2Pr0.2Nd0.2Gd0.2Tb0.2)11.76Fe82.36B5.88由于硬磁相反转与磁晶间耦合作用不同步, 导致样品在具有较大各向异性场的同时, 磁黏滞系数较小. 这表明高熵稀土永磁材料的反磁化机理与传统稀土永磁材料显著不同, 值得进一步深入研究.
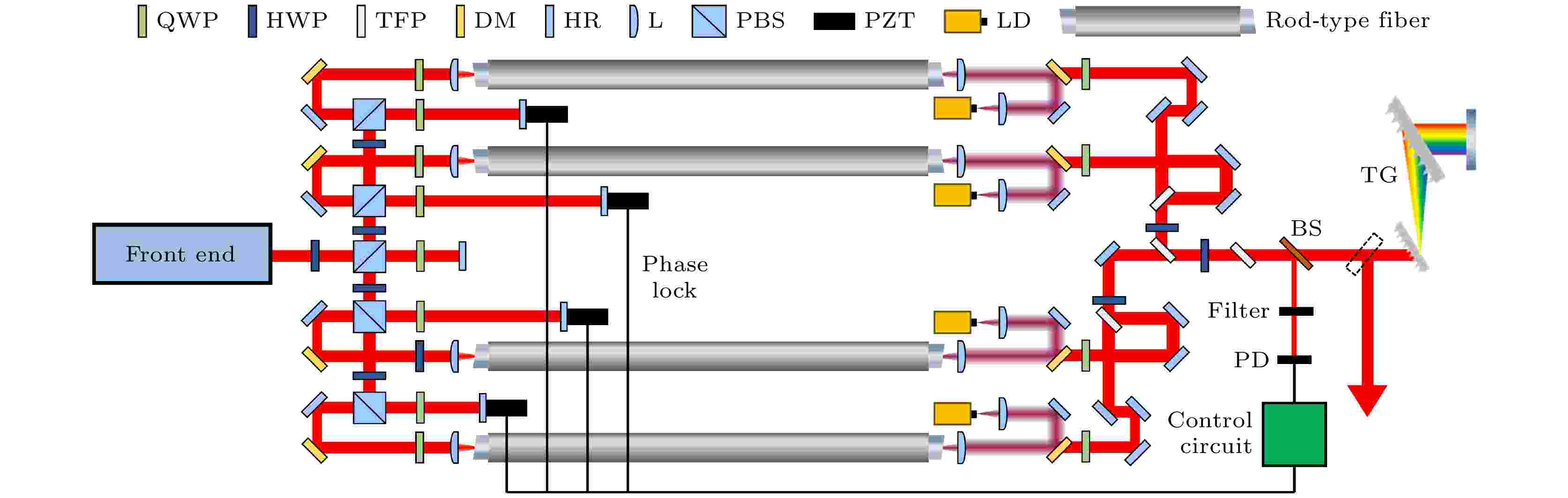
摘要 +
高平均功率(>500 W)、大脉冲能量(>1 mJ)飞秒光纤激光对包括阿秒光学在内的众多科研领域极为重要. 受限于增益光纤较小的模场面积, 多种非线性效应将从单根增益光纤放大产生的飞秒脉冲的能量限制在百微焦量级. 平均功率和脉冲能量的进一步提升需要使用相干合成技术, 将多路光纤的输出合成为一束. 本文搭建了一套基于填充孔径相干合成的高功率大能量超快光纤激光系统, 采用商用掺镱棒状光纤并利用随机并行梯度下降法实现四路放大器之间的相位锁定. 在重复频率为1 MHz时, 该相干合成系统输出平均功率为753 W, 经过光栅对压缩后的平均功率为672 W, 脉冲宽度为242 fs, 对应的脉冲能量为0.67 mJ, 系统具备良好的稳定性. 降低重复频率至500 kHz, 该系统输出压缩后的脉冲平均功率为534 W, 脉冲宽度为247 fs, 对应脉冲能量可达1.07 mJ. 脉冲的平均功率和能量均可通过增加合成路数进一步提升, 通过添加已着手研发的延迟和指向锁定系统, 有望通过八路相干合成实现平均功率超过1 kW、脉冲能量超过2 mJ的飞秒脉冲输出.
- 1
- 2
- 3
- 4
- 5
- ...
- 181
- 182