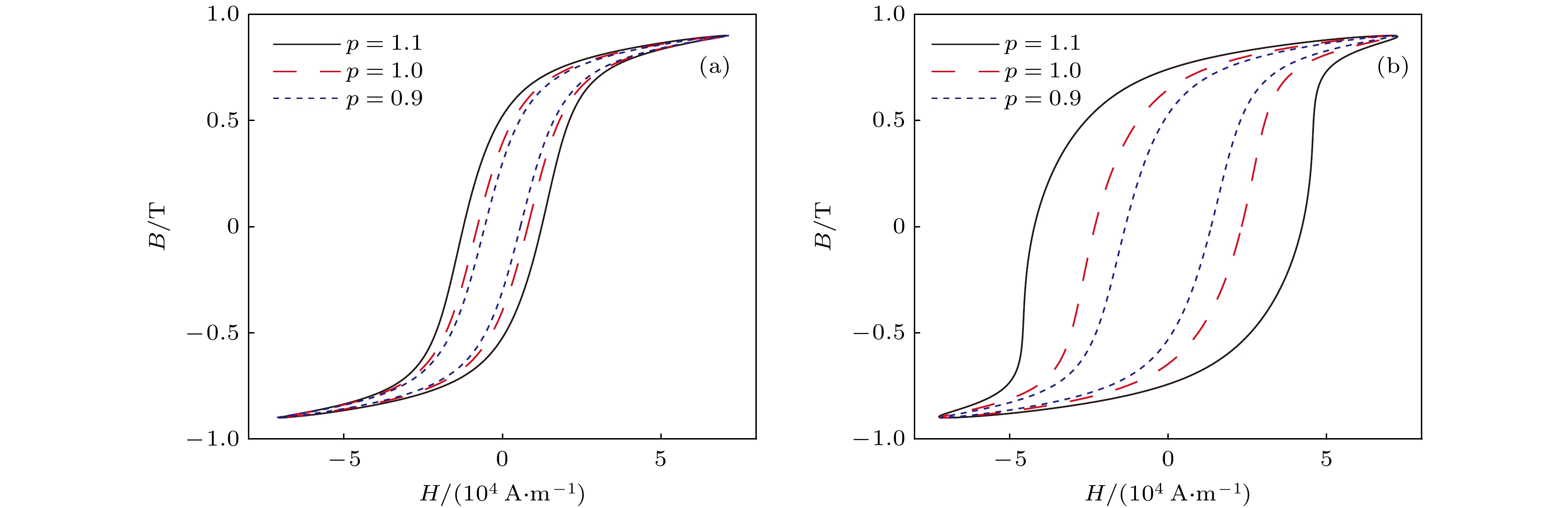
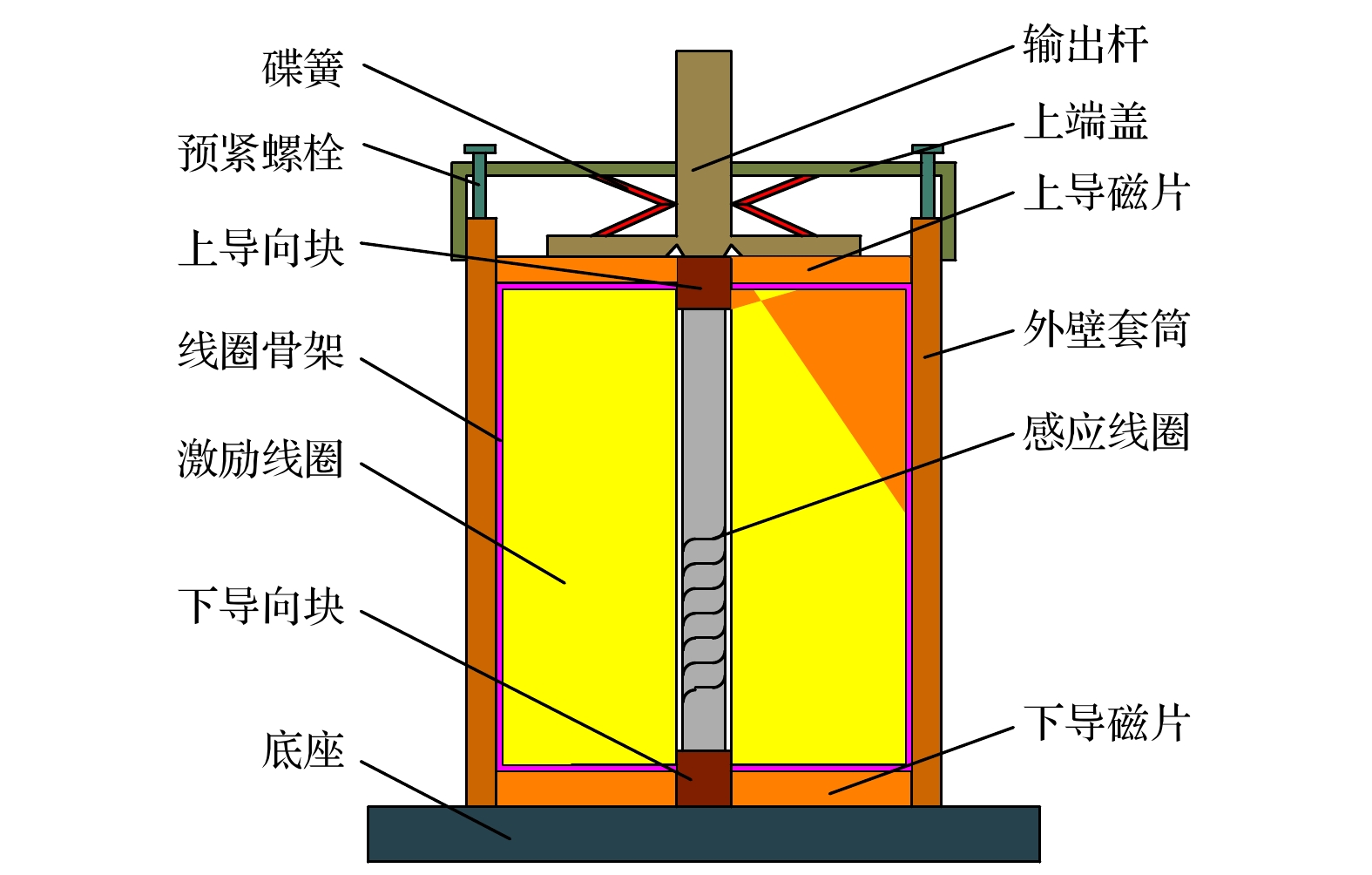
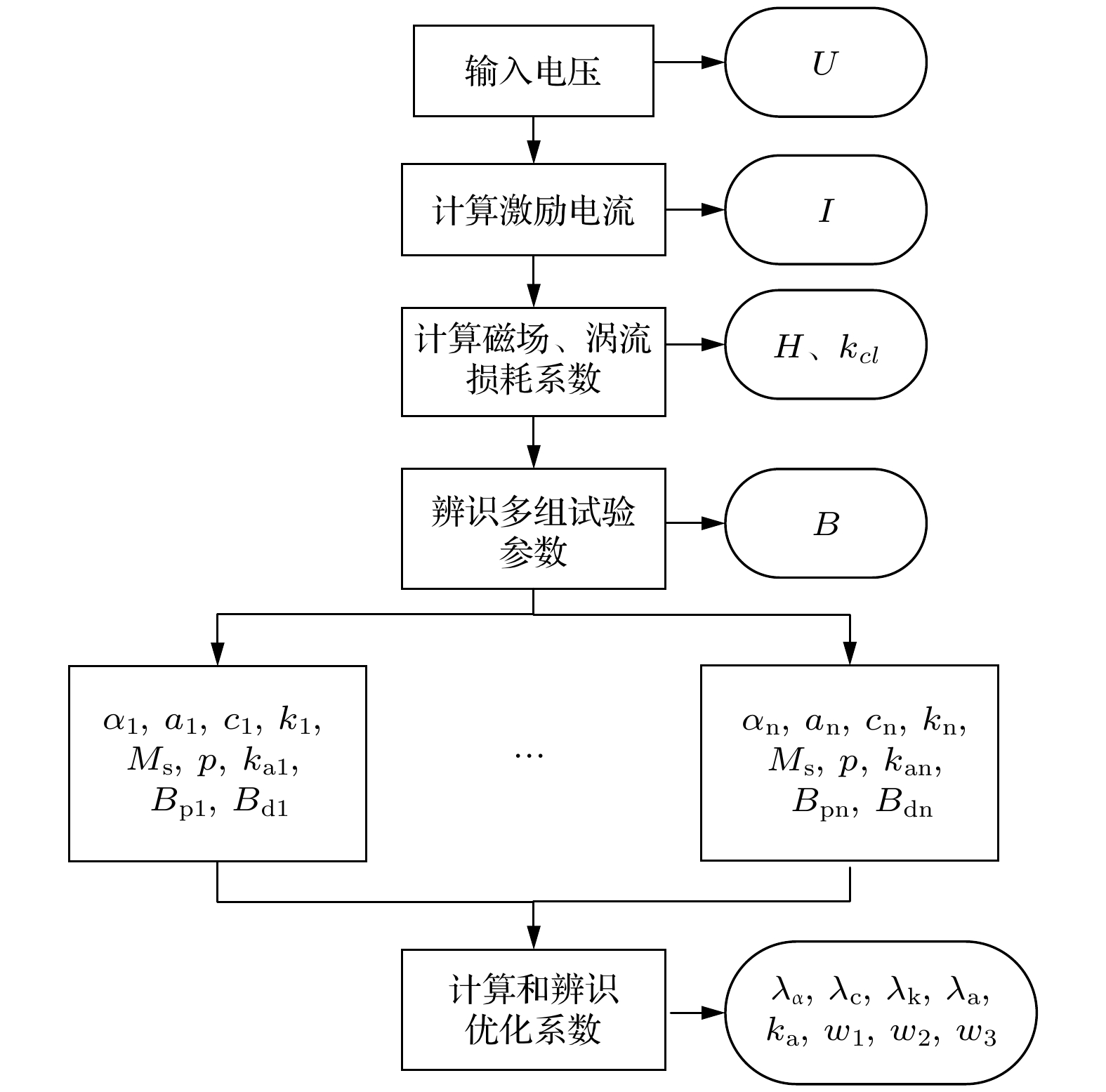
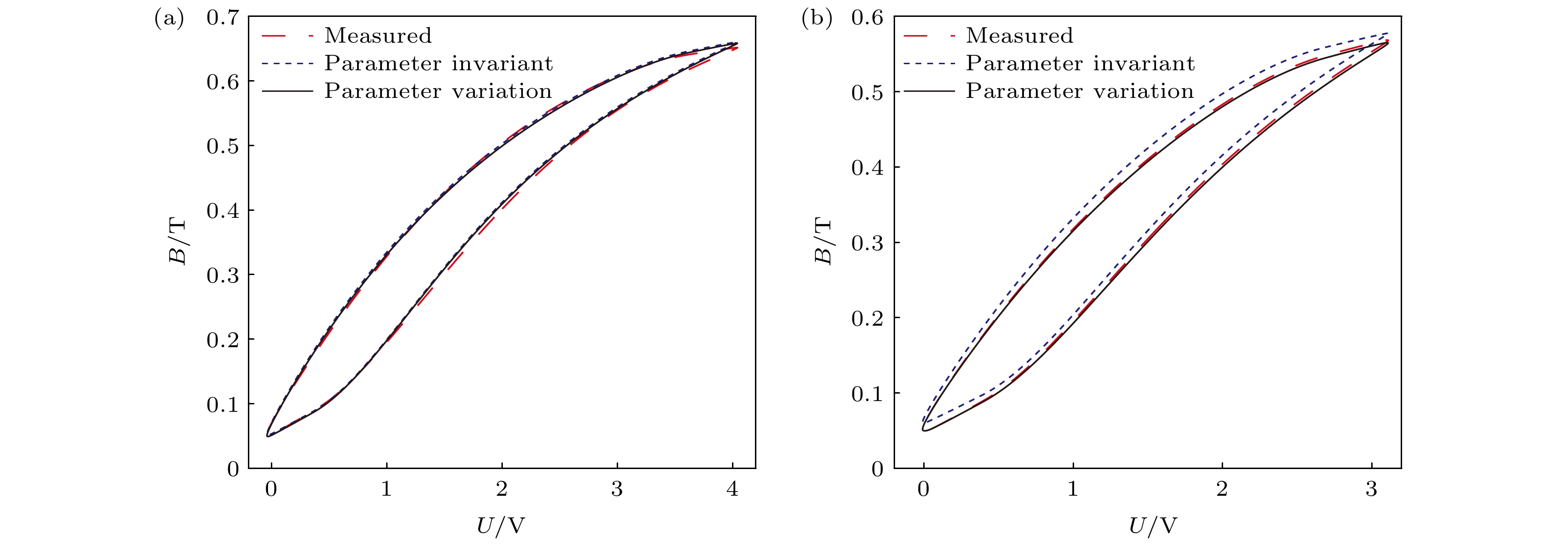
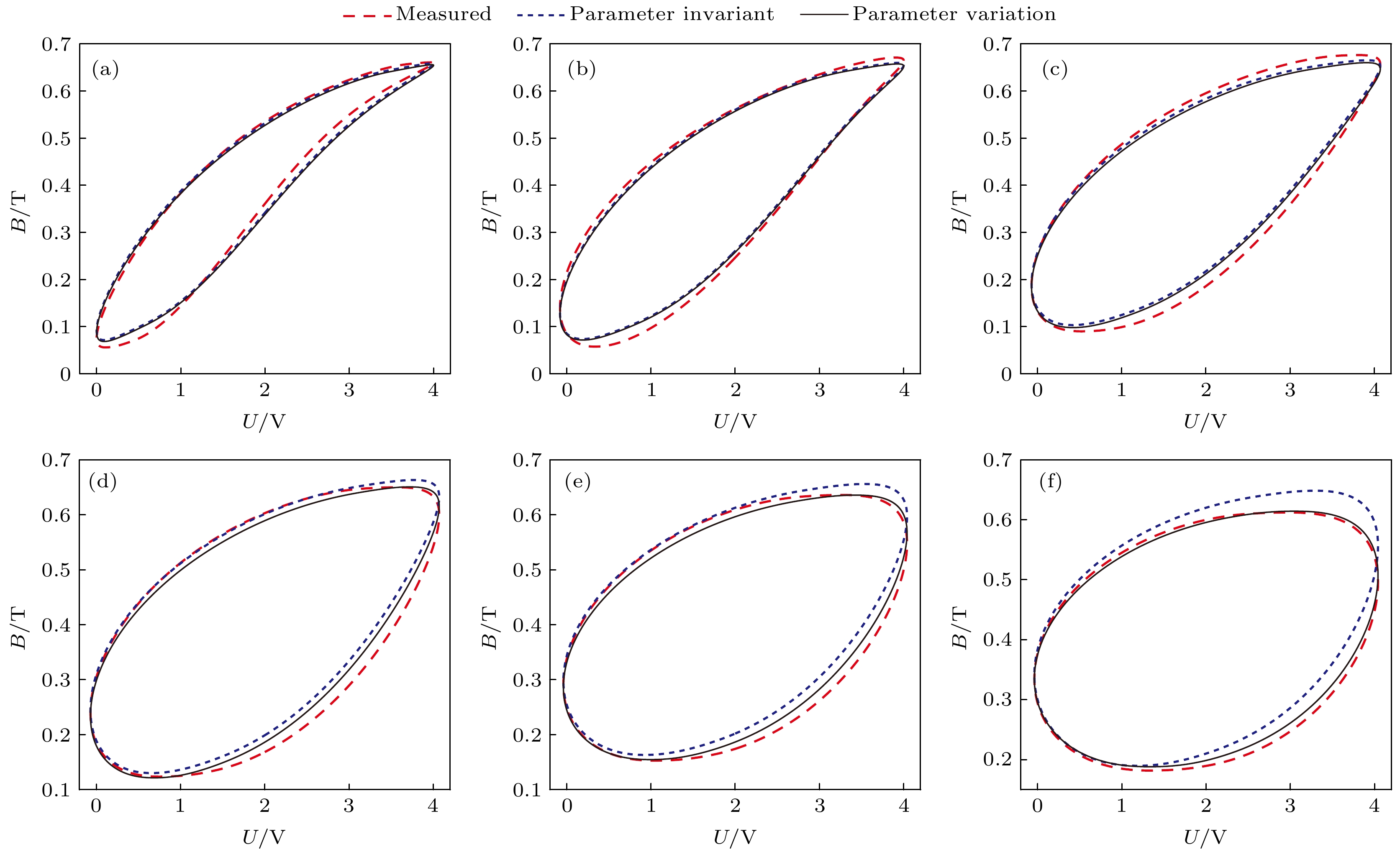
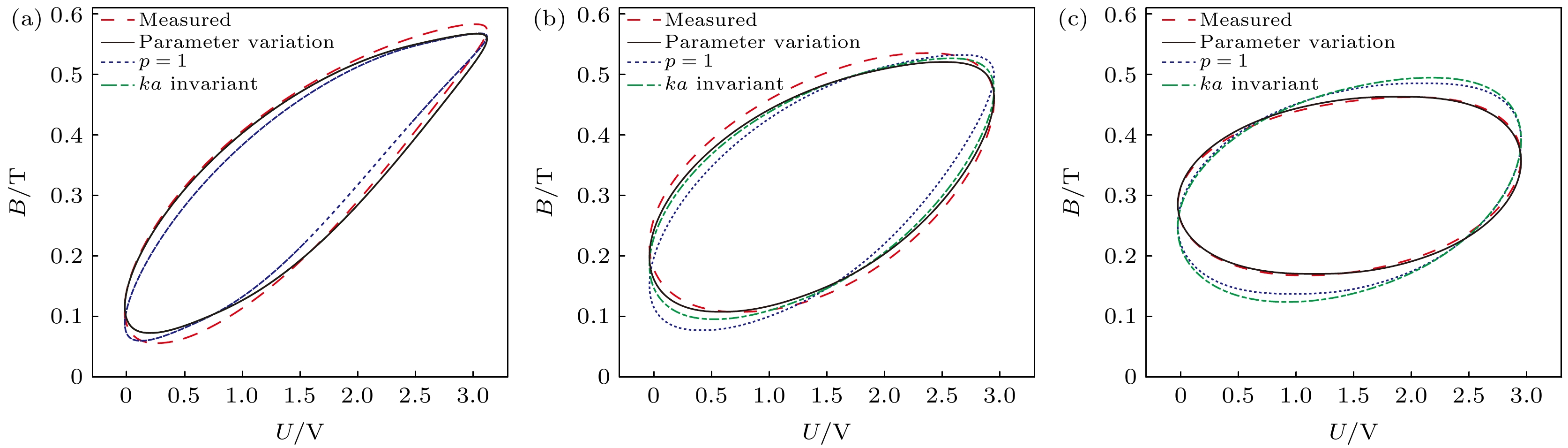
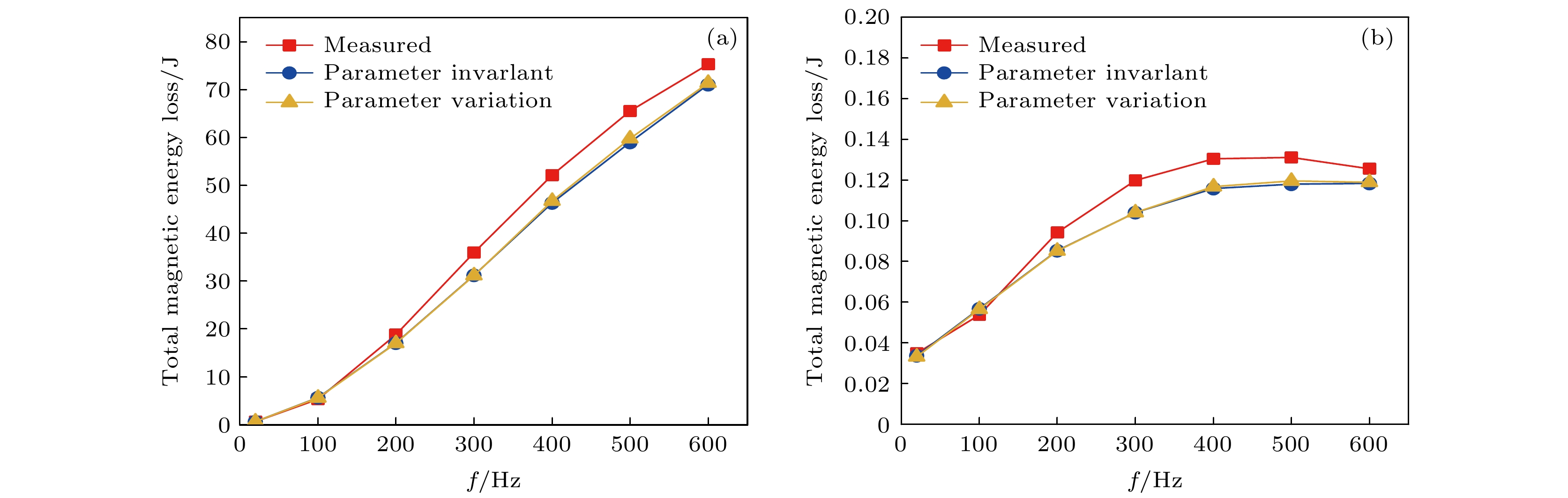
The hysteresis model of giant magnetostrictive materials (GMMs) changes with model parameters: the excitation amplitude, bias condition and excitation frequency. The existing hysteresis model is unable to predict the effects of simultaneous changes in the three external conditions. In this paper, the hysteresis loss mechanism is explained by using the traditional Jiles-Atherton (J-A) dynamic model, and the relation equation is established according to the operating conditions and material properties to respond to the changes of external conditions. For the J-A model, the relationship equation related to the excitation amplitude is established, and the relationship equation relating the residual loss coefficient to the excitation amplitude and the bias condition is established for the residual loss, while the eddy current loss of the system is redefined by using the fractional order to obtain the modified hysteresis model. In the paper, the genetic algorithm is used to identify the model parameters of the test data under different operating conditions, and the corresponding correction coefficients are obtained according to the model parameters and the operating conditions. The accuracy of the modified model is verified by simulating the model and analyzing the influences of eddy currents and residual losses and their effects on the model predictions. The hysteresis model is evaluated to compare the hysteresis curves with the hysteresis losses in terms of errors. The results show that the modified model is capable of predicting various excitations with high accuracy, and that neglecting dynamic losses at low frequencies results in large errors. If the model order of the eddy current loss is smaller than the actual order of the material, the predicted hysteresis curve will be contracted inward and the predicted eddy current loss will be small; on the contrary, the predicted hysteresis curve will be expanded outward and the predicted eddy current loss will be large, and with the increase of the excitation frequency, both cases will cause the prediction error to become larger and larger. When the bias magnetic field is zero, the residual loss coefficient is unchanged; when the bias magnetic field is kept constant, the excitation amplitude increases and the residual loss coefficient decreases; when the excitation amplitude is unchanged, the bias magnetic field increases and the residual loss coefficient also increases. When both the bias magnetic field and the excitation amplitude change at the same time, it is necessary to conduct an actual analysis of their corresponding residual loss coefficients. Using hysteresis curves to evaluate hysteresis is more accurate.













 下载:
下载: