-
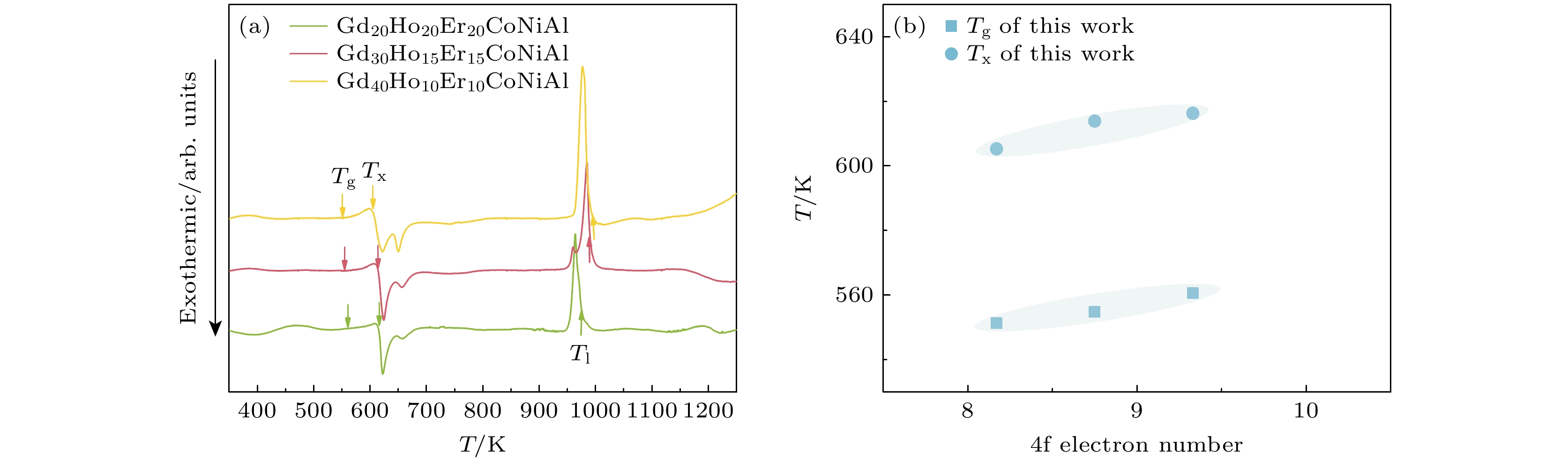
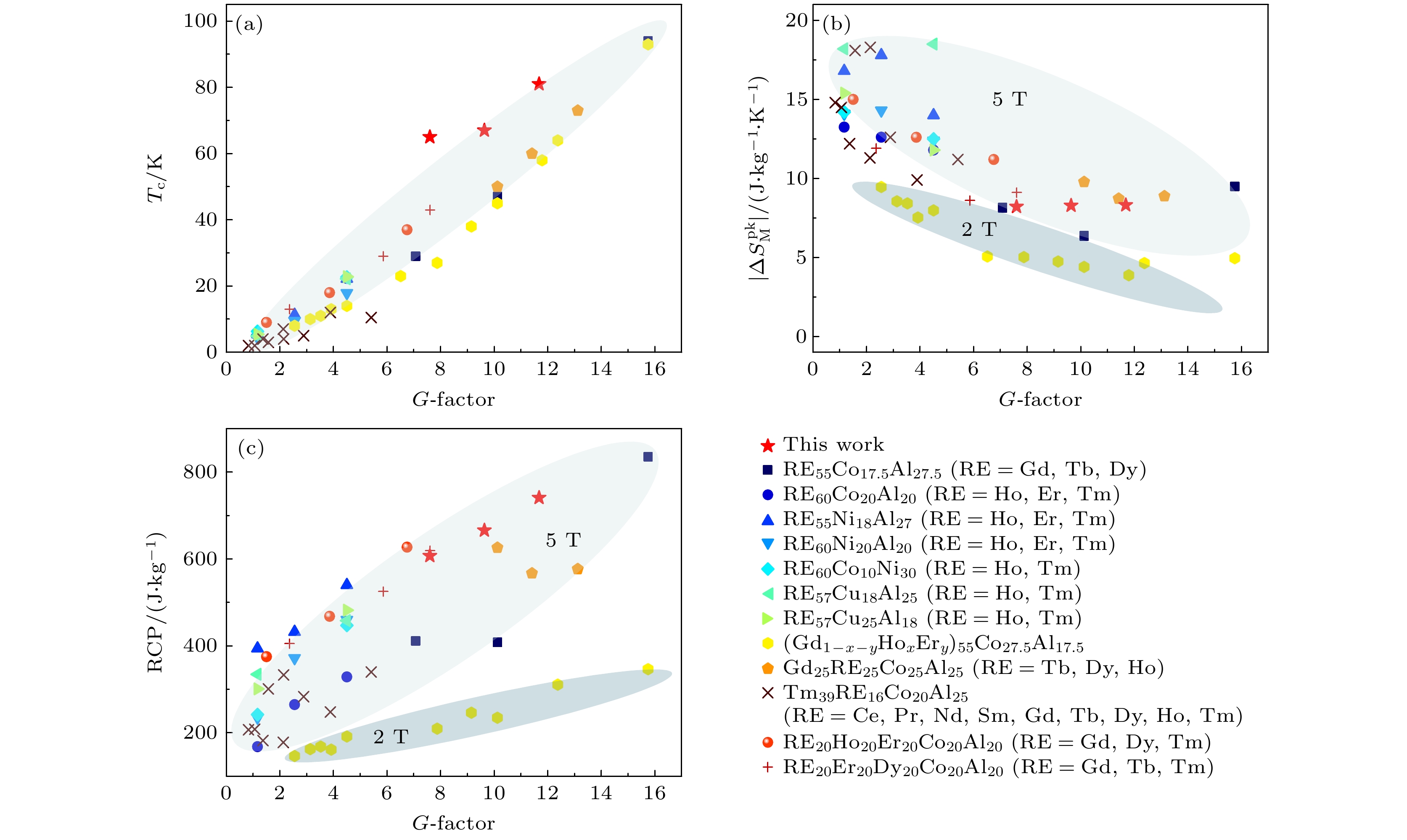
通过对Gd, Ho和Er进行元素替换, 成功设计制备出临界尺寸为2 mm的Gd 20+2xHo 20–xEr 20–xCo 20Ni 10Al 10( x= 0, 5, 10) 块体高熵非晶合金体系, 系统研究了稀土元素种类和含量对高熵非晶合金的微观结构、热力学性能和磁热性能的影响及调控机理. 研究结果表明, 随着Ho和Er逐步被Gd取代, 体系的热稳定性略有下降, 其中, 玻璃转变温度 T g和初始晶化温度 T x逐渐降低. 与此同时, 液相线温度 T l升高, 导致玻璃形成能力的热力学判据, 如约化玻璃转变温度 T rg, γ和 γ m降低. X射线和高分辨透射电子显微镜的结果分析表明, 随着Gd含量的增大, 体系的有序度减小, 有利于非晶相的生成. 另一方面, 随着Gd元素的加入, 磁热性能参量如居里温度 T c、峰值磁熵变($ | {\Delta S_{\text{M}}^{{\text{pk}}}} | $)和相对制冷能力(relative cooling power, RCP)均逐渐升高, 其中Gd 40Ho 10Er 10CoNiAl的$ | {\Delta S_{\text{M}}^{{\text{pk}}}} | $和RCP最大, 分别为8.31 J/(kg·K)和740.82 J/kg. 研究结果表明, 稀土基高熵非晶合金体系的磁热效应包括RCP, T c和$ | {\Delta S_{\text{M}}^{{\text{pk}}}} | $主要依赖于de Gennes因子, 与材料内部的有效磁矩并无直接关系, 而热力学性能主要受到4f电子引起的f-d杂化效应影响, 随着4f电子数的增加非晶合金体系的热稳定逐步增加. 综上所述, 我们可以借助稀土元素替换进行成分优选, 通过调控4f电子数获得具有较高热稳定性且 T c可调的稀土基非晶合金磁热材料.In this work, Gd 20+2xHo 20–xEr 20–xCo 20Ni 10Al 10( x= 0, 5, 10) high-entropy metallic glasses (MGs) with a critical diameter of 2 mm are successfully designed and fabricated by substituting Gd, Ho and Er. The effects of type and content of rare-earth (RE) elements on the microstructure, thermodynamic behaviors, and magnetocaloric effect (MCE) are investigated systematically. The amorphous structures of the ribbons and as-cast rods are confirmed by X-ray diffraction (XRD) with Cu Kα radiation (2 θ= 20°–80°). The atomic-scale ordered configurations are examined by using high-resolution transmission electron microscope (HRTEM). Thermal analysis is carried out on differential scanning calorimeter (DSC) with a heating rate of 20 K/min by using ribbons. The magnetic measurements are conducted by using magnetometer in a temperature range of 5–180 K. According to DSC traces, it is suggested that as Ho and Er are replaced by Gd, the thermal stability of MGs slightly decreases, for example, both glass transition temperature ( T g) and initial crystallization temperature ( T x) decrease gradually, meanwhile the liquidus temperature ( T l) increases, which results in a reduction of glass-forming ability criteria such as the reduced glass transition temperatures T rg( T rg= T g/ T l), γ( γ= T x/( T g+ T l)), and γ m( γ m= (2 T x– T g)/ T l) ,thermodynamically. The analyses based on XRD and HRTEM show that the degree of order in MGs decreases with Gd content increasing, which facilitates the glass formation. The magnetocaloric parameters such as Curie temperature ( T c), maximum magnetic entropy change ($ | {\Delta S_{\text{M}}^{{\text{pk}}}} | $) and relative cooling power (RCP) all increase gradually with the addition of Gd. The Gd 40Ho 10Er 10CoNiAl exhibits the best refrigeration performance in all studied systems, where the peak value of $ |{\Delta S}_{{\mathrm{M}}}| $ is 8.31 J/(kg·K) and RCP is 740.82 J/kg. The results indicate that MCEs of MGs including RCP, T cand $ | {\Delta S_{\text{M}}^{{\text{pk}}}} | $, mainly depend on the de Gennes factor rather than the effective magnetic moment, while thermodynamic properties are more affected by the f-d hybridization effect. As the number of 4f electrons increases, the thermal stability increases with the degree f-d orbital hybridization increasing. In summary, the RE-based MG with high thermal stability and adjustable T ccan be achieved by the RE substitution via adjusting the number of 4f electrons.
-
Keywords:
- rare-earth based high-entropy metallic glasses/
- thermodynamic properties/
- magnetocaloric effect/
- glass forming ability
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] -
Compositions ΔSconf 4f electron number Tg/K Tx/K Tl/K ΔTx/K Trg γ γm x= 0 1.748R 9.33 560.6 616.3 973.0 55.7 0.576 0.402 0.691 x= 5 1.713R 8.75 554.8 613.9 989.6 59.1 0.561 0.398 0.680 x= 10 1.609R 8.17 551.3 605.3 985.6 54.0 0.559 0.394 0.669 x ΔSconf G-factor Tc/K θ/K μeff/μB(实验) μeff/μB(理论) $ | {\Delta S_{\text{M}}^{{\text{pk}}}} | $/(J·kg–1·K–1) δTFWHM/K RCP/(J·kg–1) n N 0 1.748R 7.60 65 17.968 7.18 7.75 8.21 73.99 607.20 0.80 1.00 5 1.713R 9.64 67 77.788 6.68 7.45 8.28 80.43 665.67 0.78 1.00 10 1.609R 11.68 81 92.191 6.61 7.14 8.31 89.17 740.82 0.76 1.01 -
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73]
计量
- 文章访问数:390
- PDF下载量:11
- 被引次数:0
















 下载:
下载: