-
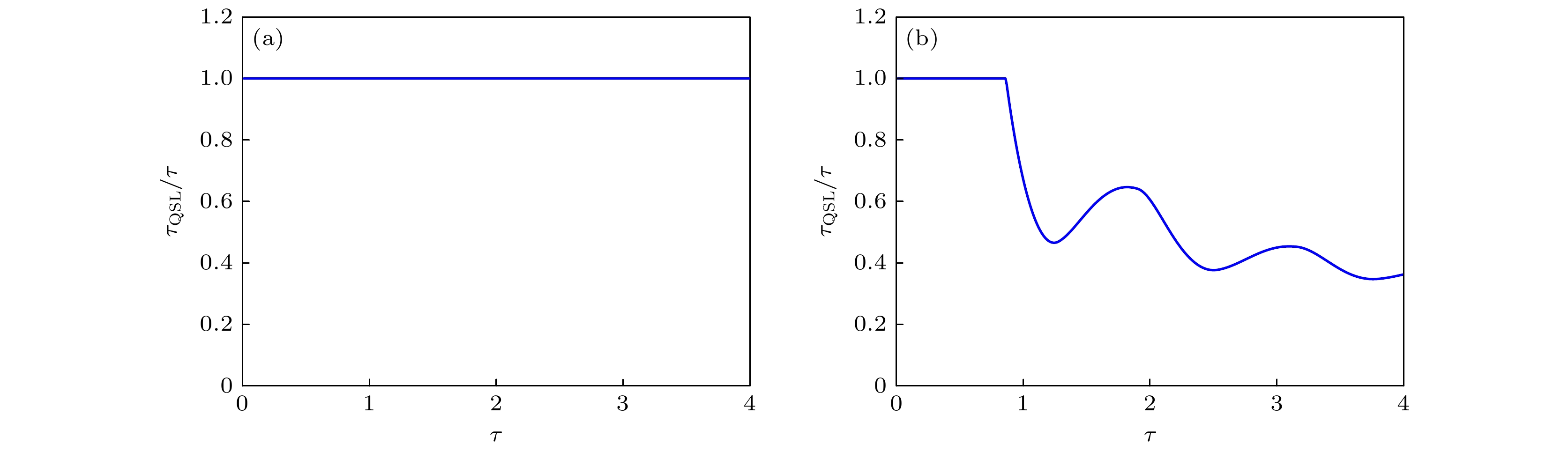
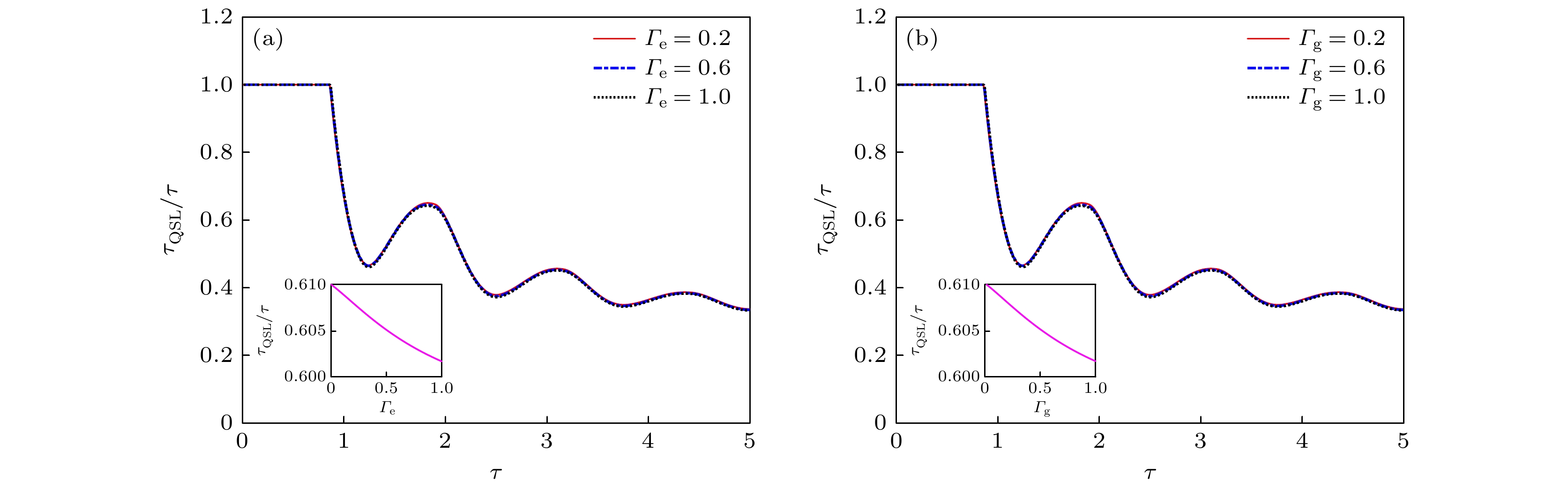
基于量子点输运理论与Bures角度量的方法, 研究了耗散环境下单量子点系统输运过程中的量子速度极限特性. 结果表明: 由于隧穿过程存在库仑阻塞效应与量子相干效应,系统可加速能力随左侧隧穿概率有微小的变化; 然而, 系统可加速能力随右侧隧穿概率变化明显, 归因于动力学通道阻塞与共隧穿的共同效应. 能级差的增大使系统向目标态演化需要更长的时间, 从而改变系统的加速潜力以及随时间演化的震荡频率. 耗散环境中弛豫速率对系统可加速能力的影响不是单调的,存在一个有趣的转折点,当弛豫速率小于该点时,系统的可加速能力产生震荡变化,当弛豫速率大于该点时,加速潜力的变化受到了弛豫速率的单调抑制,弛豫速率的增大总体上抑制了系统的可加速能力.We theoretically study the quantum speed limit (QSL) of the single dot system in dissipative environment based on quantum dot transport theory and Bures angle metric method. The theoretical results show that in the dissipative environment, different tunneling probabilities have different effects. The increase of left tunneling probability has a weak effect on the accelerating capability of the system, due to the Coulomb blocking effect and quantum coherence. On the other hand, the right tunneling probability has a significant influence on the accelerating capability of the system, the accelerating capability is promoted with the increase of right tunneling probability because of the effect of channel blocking and co-tunneling. The increase of energy displacement promotes the accelerating capability of the system and changes the oscillation frequency of the system, owing to its taking longer time for the system to evolve to a target state. The effect of the relaxation rate for the system's accelerating capability is not monotonic, there is an interesting turning point due to the change of electron layout number. When the relaxation rate is less than this point, the accelerating capability of the system will oscillate. When the relaxation rate is higher than this point, the change of accelerating capability is monotonically suppressed by the relaxation rate. In general, the increase of the relaxation rate weakens the acceleration capability of the system. Our results provide theoretical reference for studying the QSL time in a semiconductor device affected by numerous factors.
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] -
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42]
计量
- 文章访问数:2771
- PDF下载量:69
- 被引次数:0














 下载:
下载: