-
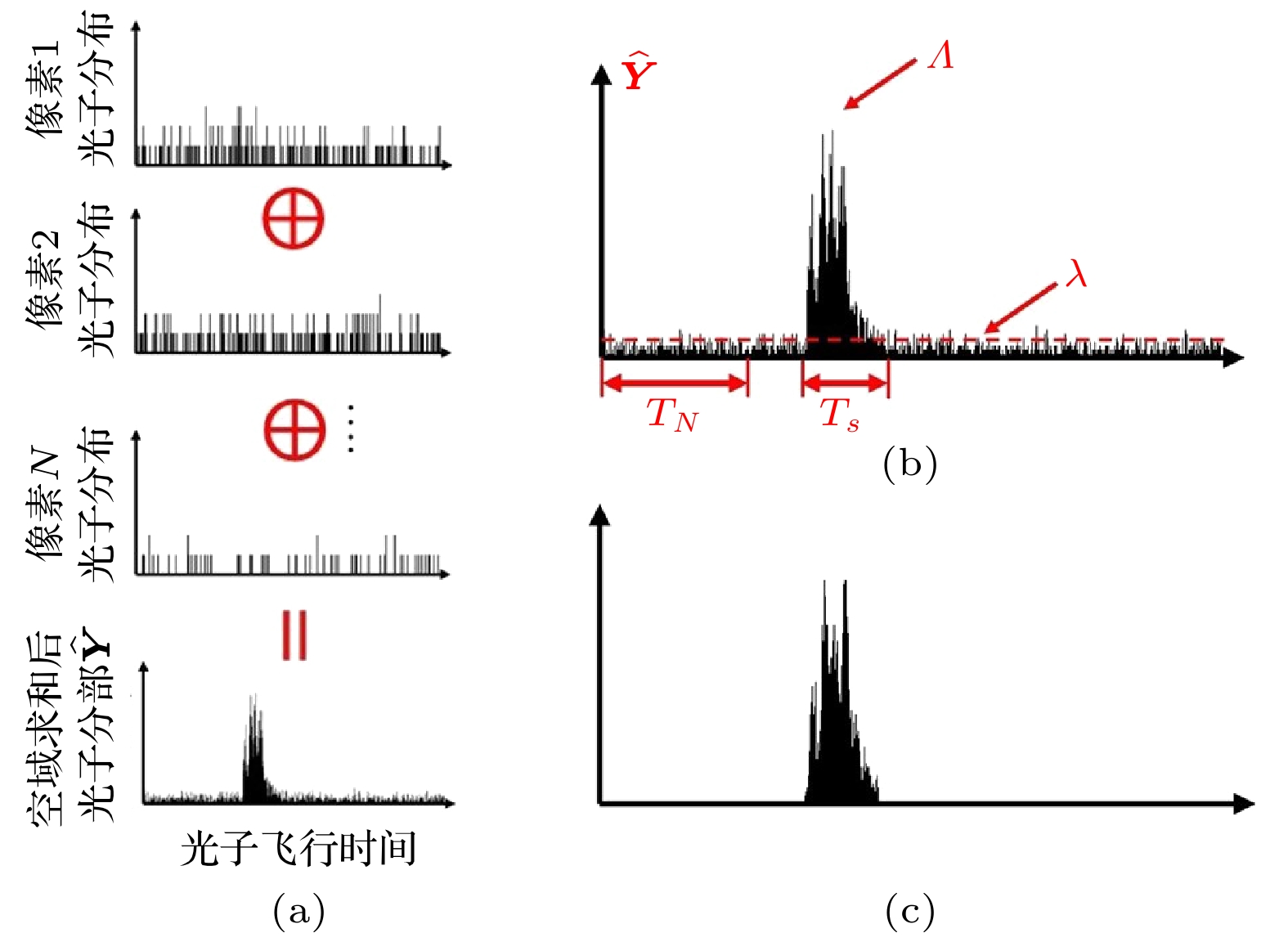
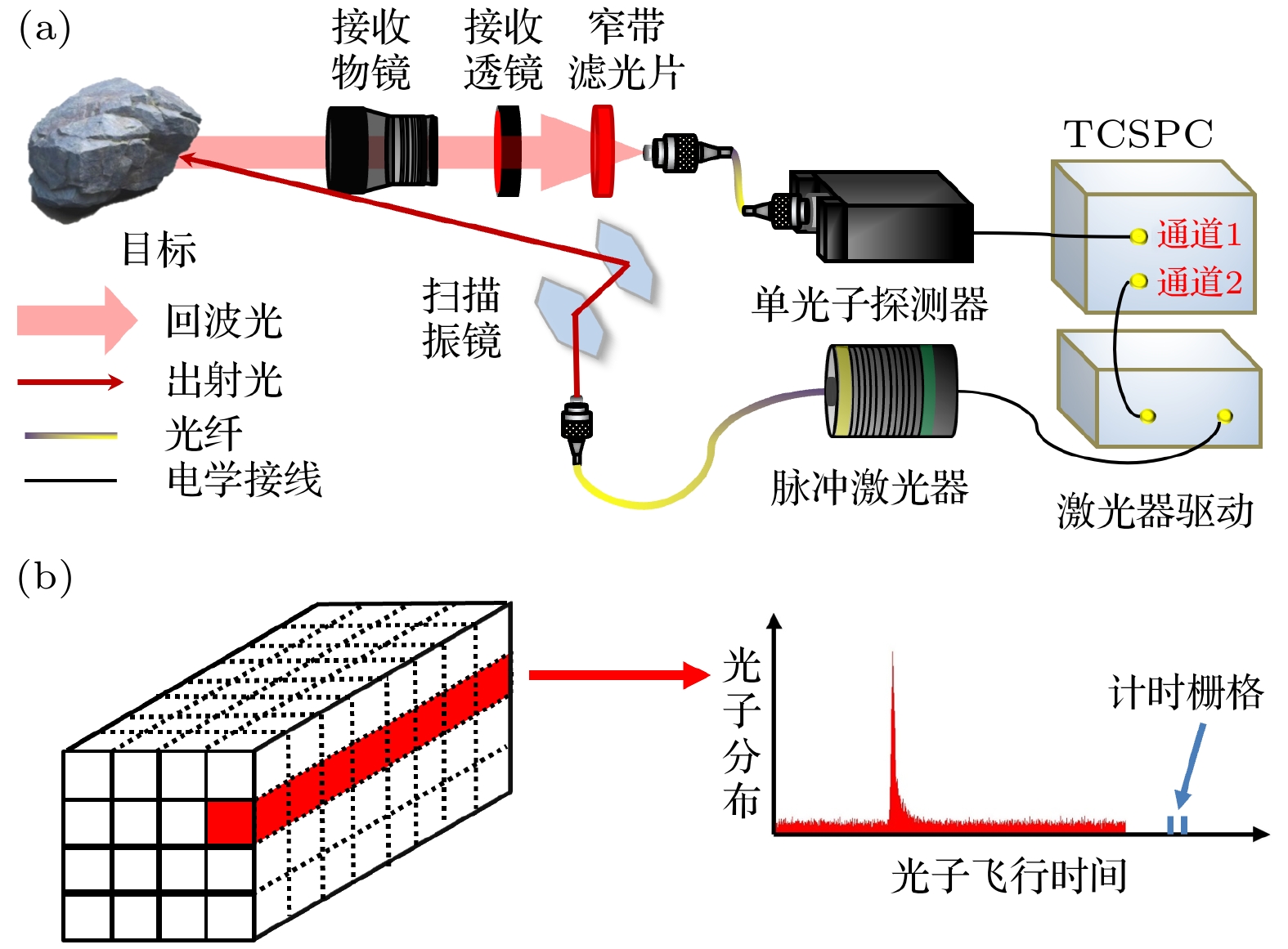
光子计数激光雷达技术具有极高的探测灵敏度与时间分辨率, 是极端条件下高精度目标信息获取的重要手段. 由于该技术通过探测单光子级的回波能量实现对目标信息的三维重建, 因此极易受噪声干扰, 导致成像质量严重降低. 基于高速电子门控的距离选通技术虽然可以有效抑制噪声, 但存在参数设计依靠经验、目标检测区间窄等问题. 本文提出一种在宽目标检测区间条件下的目标信息提取及三维重建方法, 首先通过对三维回波信息的获取机理及其概率模型进行分析, 获取目标信息分布范围并通过算法门控提取有效信息; 再采用高效的图像重建算法进一步提升三维重建的质量, 从而具有比基于纯硬件的去噪方法更强的抑噪能力. 实验结果显示, 在平均像素光子数仅为3.020, 且信号噪声比仅为0.106的极端条件下, 本文提出的目标信息提取方法可将信号噪声比提升19.330倍; 再配合高效的图像重建算法, 距离图像的重建信噪比相比于传统的互相关算法提升了33.520 dB, 大幅提升了强噪声环境下高精度目标信息获取的能力.Single photon LiDAR is considered as one of the most important tools in acquiring target information with high accuracy under extreme imaging conditions, as it offers single photon sensitivity and picosecond timing resolution. However, such technique sense the scene with the photons reflected by the target, thus resulting in severe degradation of image in presence of strong noise. Range gating with high-speed electronics is an effective way to suppress the noise, unfortunately, such technique suffers from manually selecting the parameters and limited gating width. This paper presents a target information extracting and image restoration method under large observation window, which first obtain the depth distribution of the target and extract the information within the range by analyzing the model of signal and noise, then further improve the image quality by adopting advanced image restoration algorithm and henceforth shows better results than those denoising method that purely relying on hardware. In the experiment, photon-per-pixel (PPP) was as low as 3.020 and signal-to-background ratio (SBR) was as low as 0.106, the proposed method is able to improve SBR with a factor of 19.330. Compared to classical algorithm named cross correlation, the reconstruction signal to noise ratio (RSNR) increased 33.520dB by further cooperating with advanced image restoration algorithm, thus improved the ability of sensing accurate target information under extreme cases.
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] -
Algorithm 1基于自适应门控的噪声抑制(AGNR)算法 1: 输入: $ \widehat{{\boldsymbol Y}} $,γ,ω,σ
2: 初始化$ T_N $,N,λ, Λ, PPP, SBR, $\varepsilon$, $ i = 1 $
3: $\theta=\lambda \times N+(\varLambda-\lambda \times N) \times \frac{\omega}{\gamma}{\rm{e}}^{(-\frac{{\rm{SBR}}}{\gamma})}$
4:while$ i = 1 $do
5: $ \{{\boldsymbol{\zeta}} = [T_a, T_b]\} \leftarrow (\widehat{{\boldsymbol Y}} > \theta) $
6: $E=|\sum_{i = T_a}^{T_b}\widehat{ {\boldsymbol Y} }-[{\rm{PPP}}+\lambda \times (T_b-T_a)] \times N|$
7: $T_{\rm{c} }= \Big\lceil \dfrac{E}{ \langle (\gamma/T) \times{\rm{ PPP} }, \lambda \rangle } \Big\rceil,$
8: $(\theta_1, \theta_2) \leftarrow [(\underrightarrow{\zeta})_{T_{\rm{c}}}, (\underleftarrow{\bar{\zeta} })_{T_{\rm{c}}}]$
9: 根据(7)式与(8)式计算$ E_1 $与$ E_2 $
10: $ \theta=(\theta_1, \theta_2) \leftarrow \lfloor E_1, E_2 \rfloor $
11:if$ E < \epsilon $then
12: $ i = 0 $
13:end if
14:end while
15: $ ({\boldsymbol{\zeta}} > \gamma) \leftarrow 0 $
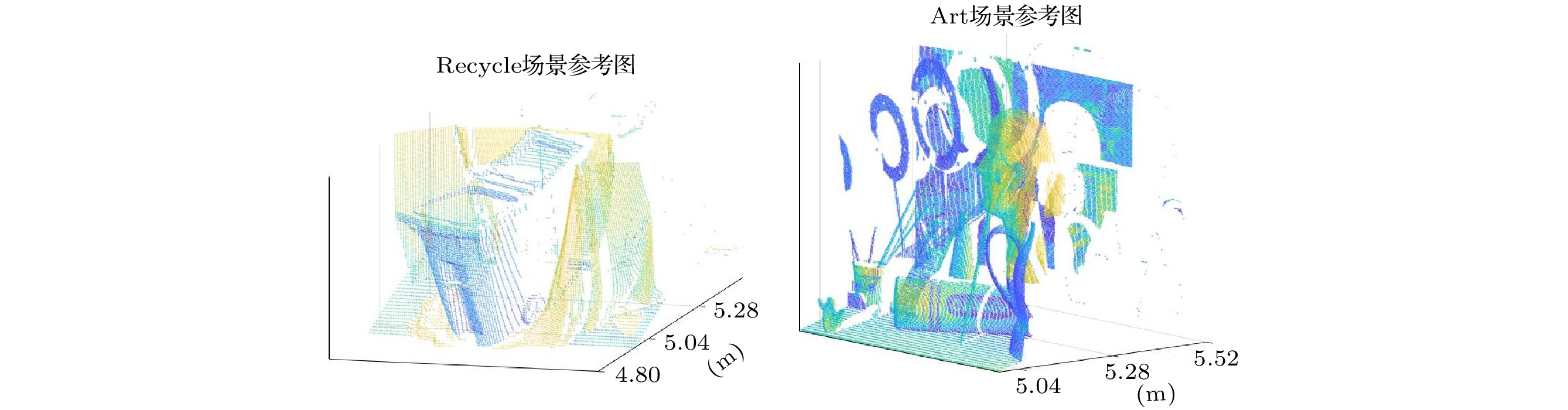
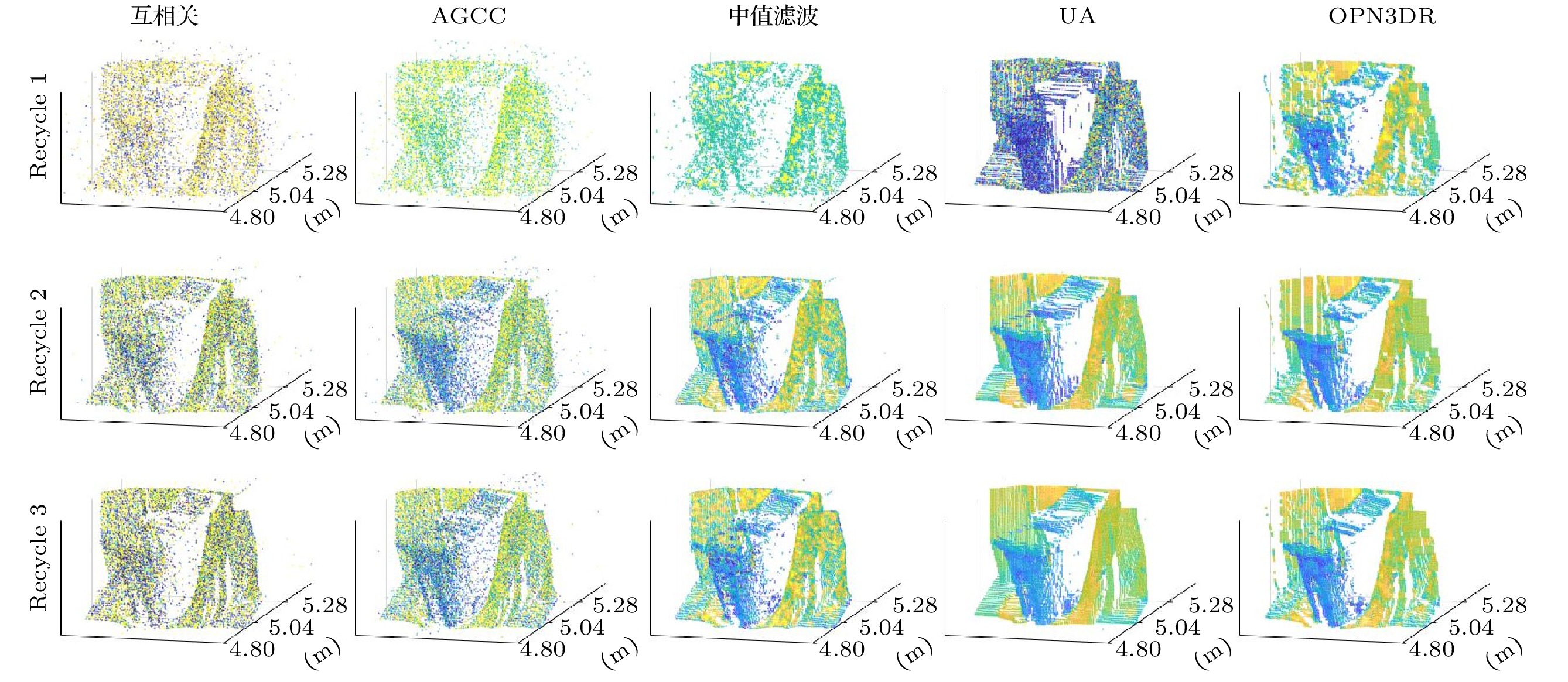
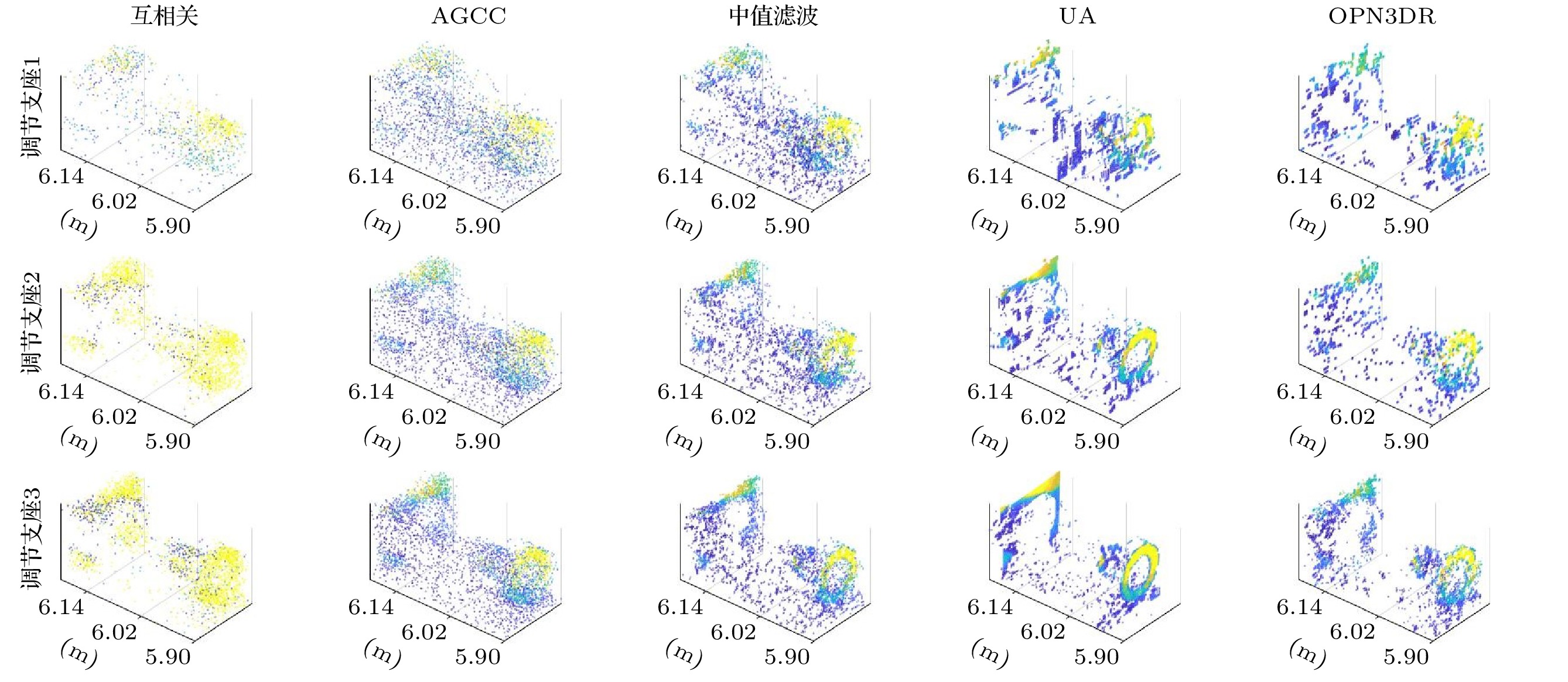
16: $ {\boldsymbol{\zeta}} \leftarrow \{[{\boldsymbol{\zeta}}-\sigma] \cup [{\boldsymbol{\zeta}}+\sigma\} $场景 Recycle Art 调节支座 Recycle1 Recycle2 Recycle3 Art1 Art2 Art3 调节支座1 调节支座2 调节支座3 PPP 0.951 6.226 12.727 0.833 4.664 11.553 3.020 30.044 150.144 SBR 0.581 0.127 0.031 0.013 0.114 0.014 0.106 0.104 0.104 $\textrm{SBR}^{’}$ 6.435 1.431 0.363 0.222 1.931 0.250 2.049 2.050 2.029 NRR ${11.076}$ ${11.268}$ ${11.710}$ ${17.077}$ ${16.939}$ ${17.857}$ ${19.330}$ ${19.712}$ ${19.510}$ 场景 评价对象 Recycle Art 调节支座 Recycle1 Recycle2 Recycle3 Art1 Art2 Art3 调节支座1 调节支座2 调节支座3 互相关 距离图 $-9.743$ $-8.533$ $-8.231$ $-15.597$ $-10.482$ $-10.848$ $-4.932$ $-3.023$ $-1.338$ 反射率图 $-4.101$ $-0.908$ $-3.691$ $-21.453$ $-3.504$ $-8.024$ $4.533$ $4.687$ $4.698$ AGCC 距离图 $11.524$ $17.961$ $17.577$ $12.862$ $19.789$ $19.633$ $22.352$ $24.751$ $26.369$ 反射率图 $0.114$ $6.433$ $6.062$ $-7.806$ $4.175$ $3.457$ $5.324$ $7.504$ $7.731$ 中值滤波 距离图 $13.954$ ${22.304}$ ${21.881}$ $18.552$ $27.340$ $26.903$ $24.389$ $25.909$ $26.788 $ 反射率图 $5.844$ $12.608$ $12.284$ $2.316$ ${10.584}$ $10.261$ $8.383$ $9.500$ $9.571$ UA 距离图 ${20.768}$ $21.318$ $21.321$ $20.519$ $24.761$ $24.764$ ${28.588}$ ${28.741}$ ${29.199}$ 反射率图 $3.304$ ${16.755}$ ${18.760}$ $5.513$ $10.034$ ${11.122}$ ${7.926}$ ${9.677}$ ${9.890}$ OPN3DR 距离图 $20.075$ $21.430$ $21.172$ ${22.767}$ ${27.453}$ ${27.397}$ $25.726$ $26.801$ $28.298$ 反射率图 ${11.093}$ $15.812$ $15.380$ ${8.910}$ $10.448$ $10.255$ $7.915$ $8.979$ $9.004$ 场景 Recycle Art 调节支座 ${\rm{Recycle1}}$ ${\rm{Recycle2}}$ ${\rm{ Recycle3}}$ ${\rm{Art1}}$ ${\rm{ Art2 }}$ ${\rm{Art3}}$ 调节支座1 调节支座2 调节支座3 互相关 0.679 0.690 0.711 2.663 2.693 2.720 0.273 0.260 0.286 AGCC 0.085 0.085 0.085 0.220 0.224 0.218 0.023 0.024 0.024 中值滤波 0.095 0.096 0.096 0.235 0.239 0.234 0.035 0.035 0.036 UA 6.290 7.759 10.787 20.335 13.517 19.832 4.320 5.073 8.711 OPN3DR 1.422 1.344 1.986 5.464 5.518 5.228 0.145 0.228 0.724 场景 评价对象 距离图RSNR 反射率图RSNR 运行
时间/s调节支座1 多尺度滤波 ${27.441}$ $0.125$ $0.785$ 最大尺度滤波 $25.726$ ${7.915}$ ${0.145}$ 调节支座2 多尺度滤波 ${29.273}$ $1.218$ $0.772$ 最大尺度滤波 $26.801$ ${8.979}$ ${0.228}$ 调节支座3 多尺度滤波 ${30.552}$ $7.030$ $0.781$ 最大尺度滤波 $28.298$ ${9.004}$ ${0.724}$ -
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21]
计量
- 文章访问数:4512
- PDF下载量:114
- 被引次数:0













 下载:
下载: