-
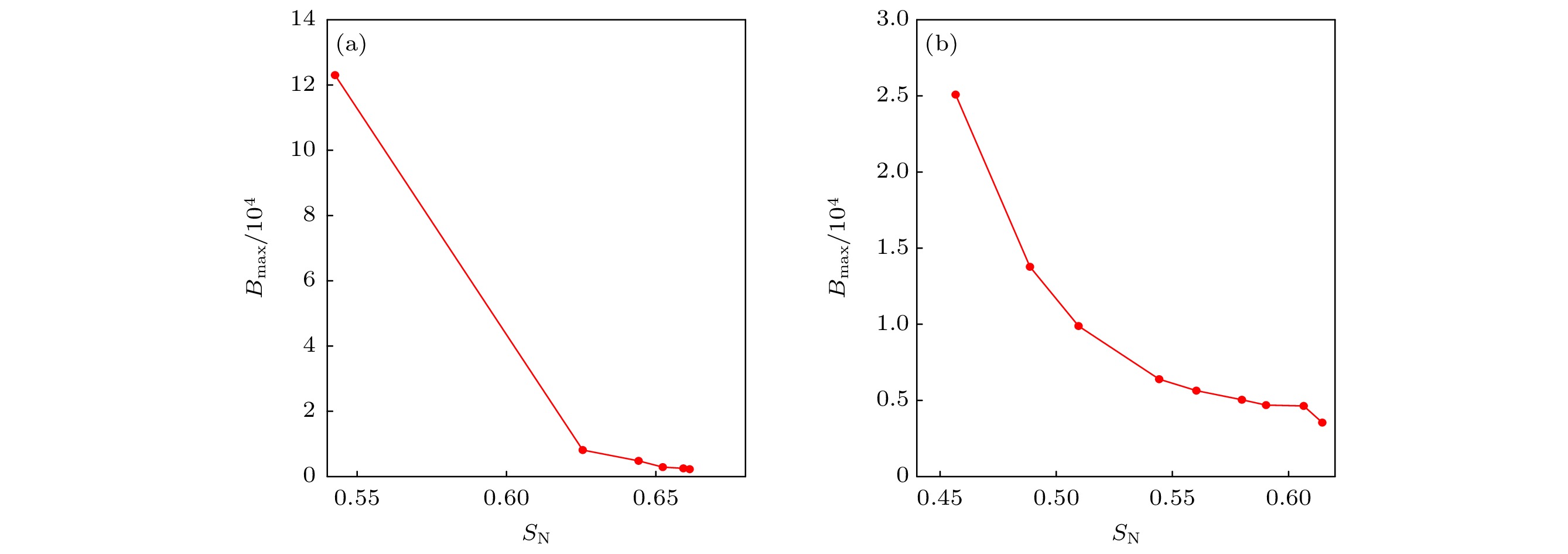
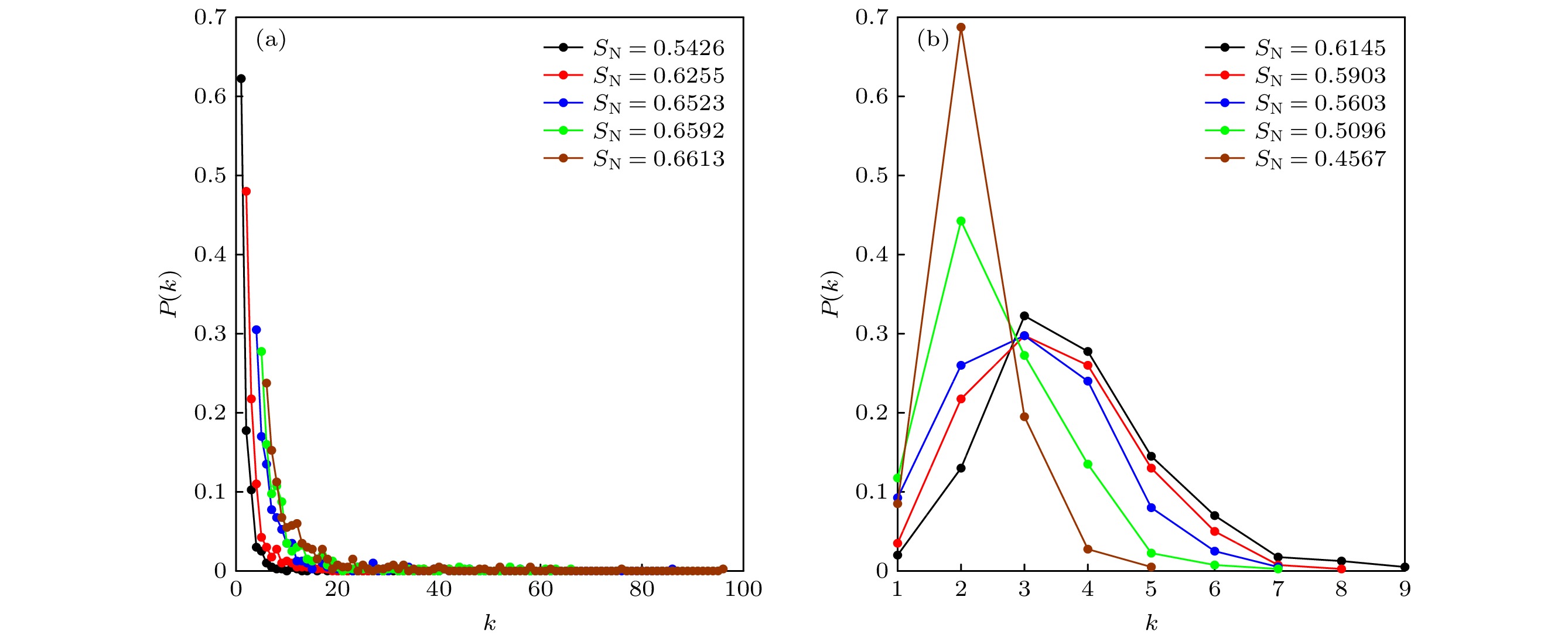
网络的传输性能在一定程度上依赖于网络的拓扑结构. 本文从结构信息的角度分析复杂网络的传输动力学行为, 寻找影响网络传输容量的信息结构测度指标. 通信序列熵可以有效地量化网络的整体结构信息, 为了表征网络整体传输能力, 把通信序列熵引入到复杂网络传输动力学分析中, 研究网络的通信序列熵与传输性能之间的关联特性, 分析这种相关性存在的内在机理. 分别在BA无标度和WS小世界网络模型上进行仿真, 结果显示: 网络的通信序列熵与其传输容量存在密切关联性, 随着通信序列熵的增加, 网络拓扑结构的均匀性随之增强, 传输容量明显增加. 网络的传输容量是通信序列熵的单调递增函数, 与通信序列熵成正关联关系. 通信序列熵可有效评估网络的传输容量, 本结论可为设计高传输容量网络提供理论依据.The transmission performance of the network depends to a certain extent on the topology of the network. This article analyzes the traffic dynamics of complex networks from the perspective of structural information, and looks for information structure measurement indicators that affect network traffic capacity. Existing research shows that the communicability sequence entropy of complex networks can effectively quantify the overall structure of the network. Based on this measurement, the difference between networks can be effectively quantified, and the connotation of sequence entropy of communicability can be explained. Communication sequence entropy can effectively quantify the overall structure information of the network. In order to characterize the overall traffic capacity of the network, the communication sequence entropy is introduced into the phenomenon of complex network congestion, the correlation between the network communication sequence entropy and the transmission performance is studied, and the internal mechanism of this correlation is analyzed. Simulations in BA scale-free network model and WS small-world network model show that the communication sequence entropy of the network is closely related to its traffic capacity. As the communication sequence entropy increases, the uniformity of the network topology will increase, and the traffic capacity will increase significantly. The traffic capacity of the network is a monotonically increasing function of the entropy of the communication sequence, and is positively correlated with the entropy of the communication sequence. The communication sequence entropy of the network can effectively evaluate the traffic capacity of the network. This conclusion can provide a theoretical basis for the design of a high traffic capacity network and help provide an effective strategy for the design of the high traffic capacity of the network, which can be optimized by increasing the communication sequence entropy.
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] -
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54]
计量
- 文章访问数:5309
- PDF下载量:138
- 被引次数:0













 下载:
下载: