-
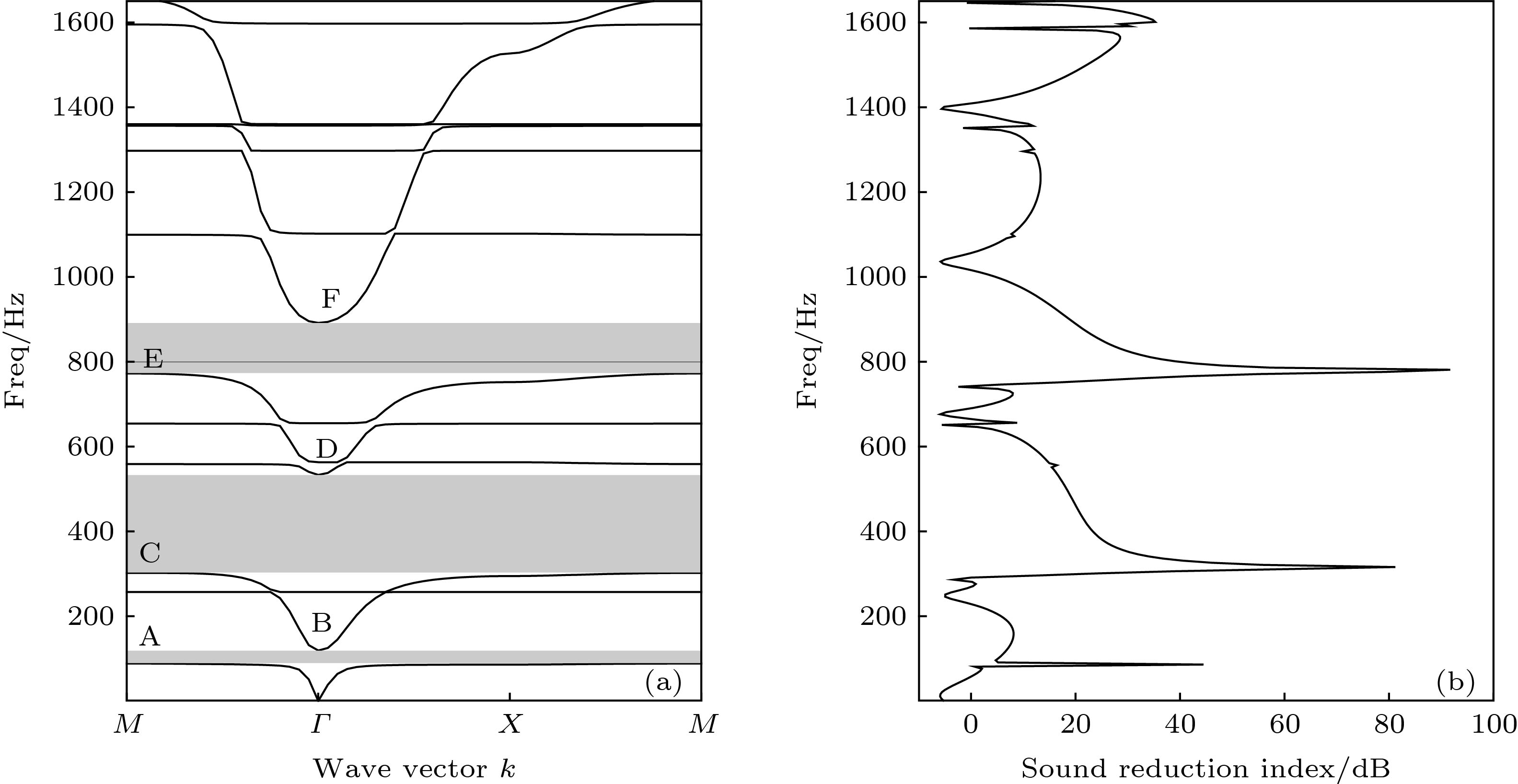
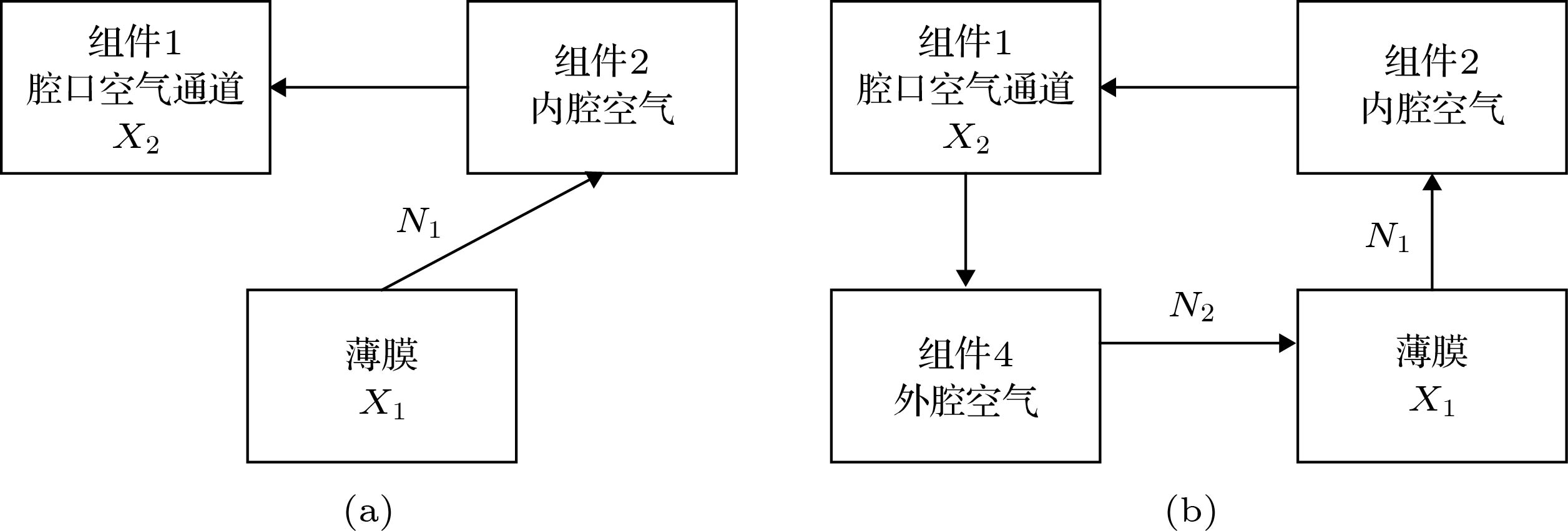
设计了一种含薄膜壁的Helmholtz型声子晶体, 该结构利用了空气和薄膜的耦合振动, 一方面将刚性壁转变为柔性壁, 降低了一阶振动时的等效刚度, 使第一带隙下限分别低于同参数下的普通Helmholtz型声子晶体和薄膜, 另一方面基于局域共振原理, 由于薄膜的出现和腔口空气通道长度的增加, 使得结构在低频范围内存在多个振动模态, 从而将原有一个带隙扩展为多个带隙. 将该结构带隙上下限分别等效为环形系统和串联系统, 用传递矩阵法和有限元法两种方法计算了其低频带隙范围, 两种方法结果吻合良好. 通过调整参数对带隙调控规律进行了进一步分析, 结果显示, 在低频范围内, 既可以通过改变与腔口空气通道或薄膜相关的参数, 在保证其中某些带隙变化不大的情况下, 单独调整其他带隙; 也可以通过调整内外腔体积, 对所有带隙进行调控.
-
关键词:
- Helmholtz共振腔/
- 低频带隙/
- 噪声控制/
- 声子晶体
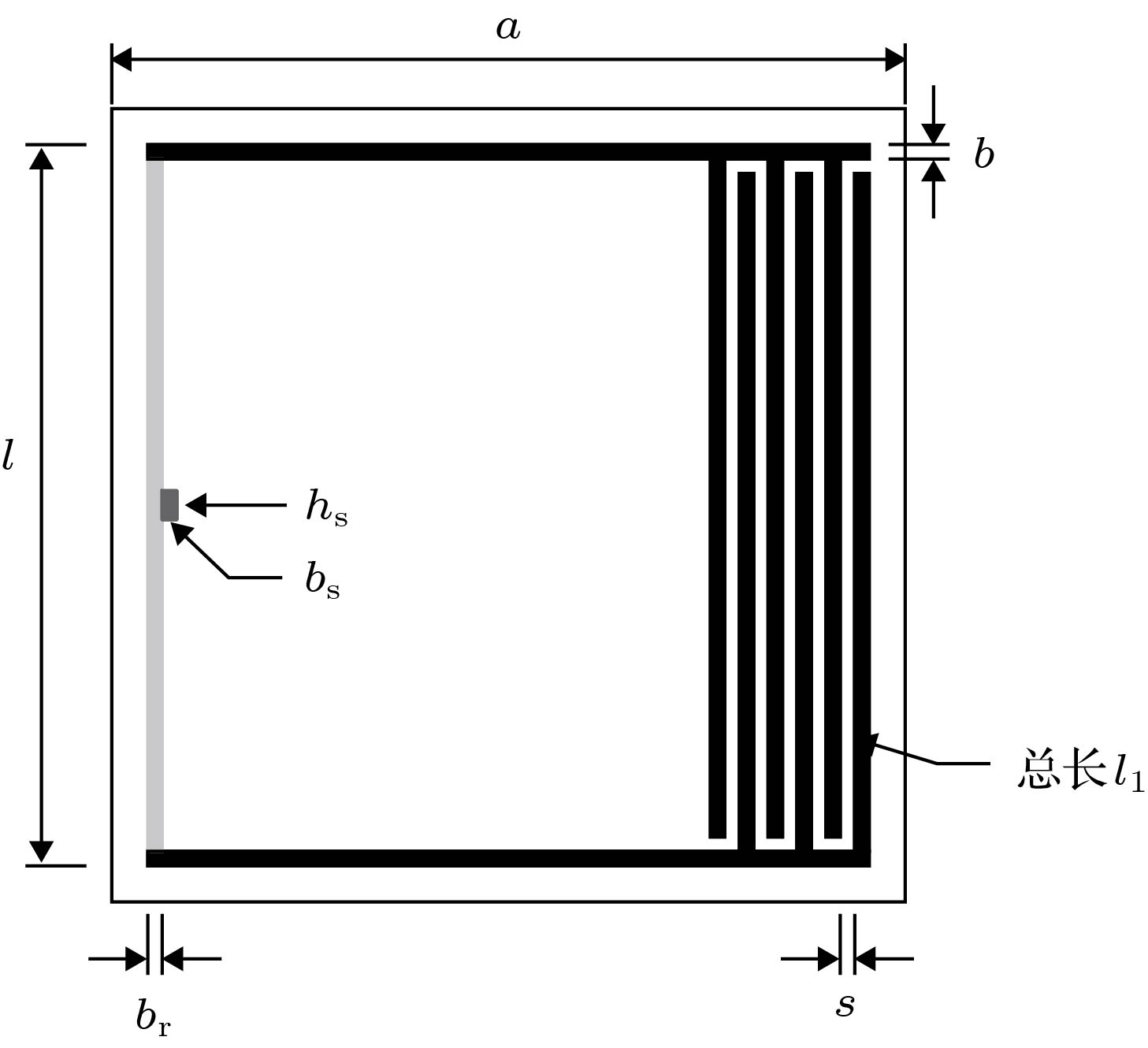
In this paper, a phononic crystal is designed using a Helmholtz resonator with a membrane wall, in which the coupled vibration of air and membrane is utilized. The structure of the Helmholtz resonator is a two-dimensional structure. On the basis of the square Helmholtz resonator, a " W”-type outlet is used as a cavity outlet to increase the air quality involved in resonance, and the cavity wall is replaced with a membrane with distribution mass to increase the number of resonance units. The finite element method is used to calculate the band gaps and transmission loss of sound below 1700 Hz. The results show that the starting frequency of the first band gap of the structure is further reduced. At the same time, it is lower than the starting frequency of ordinary Helmholtz structure and the natural frequency of membrane under the same conditions. Then, a new peak of transmission loss is obtained, and its value is greater than the original structure’s. And although the width of the first band gap is reduced, some new band gaps appear in the low-frequency range, so that the total band gap width is improved. By analyzing the vibration mode of the membrane and sound pressure distribution, it is found that the sum of the sound pressures of the outer cavity is zero at the starting frequencies of the band gaps, and the sound pressure of the inner and outer cavity are respectively positive and negative at the cut-off frequency. With the increase of frequency, the vibration mode of the membrane gradually turns from low-order to high-order, but no anti-symmetric-type mode participation is found at the starting and cut-off frequency. The components of the structure can be made equivalent to corresponding ones, respectively, i.e. air in the outlet is equivalent to uniform flexible rod, and the air in the inner and outer cavity are equivalent to a spring. So that the structure can be equivalent to a series system consisting of a rod, a spring and a membrane at starting frequency of the band gap, and a loop system consisting of a rod, two springs and a membrane at cut-off frequency. Thus, by the transfer matrix method and the Rayleigh-Ritz method considering the influence of tension and elastic modulus, it is possible to calculate the range of band gap which is extremely close to the result from the finite element method. Through the analysis of the formulas, it can be found that the new band gap is caused by the new vibration mode produced by the membrane or the air in the cavity outlet, and the lower starting frequency of the first band gap is due to the reduction of the equivalent extent of the system by the membrane. By adjusting the relevant parameters of the membrane and the cavity outlet respectively, it can be found that the band gaps of the structure correspond to the modes of different orders of the air in the cavity outlet and the membrane. In other words, the change of the natural frequency of a certain mode of air in the outlet or membrane only has a greater influence on the corresponding band gap but has less influence on other band gaps, also, the trends of change are the same, and the change values are very close to each other. But, changing the volume of the inner cavity and the outer cavity has a great influence on all the band gaps. Therefore, it is possible to adjust some band gaps through this method. [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] -
ls/10–3m 4 6 8 10 12 14 1阶固有频率 252.4 237.9 226.8 218.2 211.6 206.6 2阶固有频率 751.3 782.8 794.0 814.8 843.4 879.1 ls/10–3m 第一带隙下限 第一带隙上限 第二带隙下限 第二带隙上限 第三带隙下限 第三带隙上限 FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% 4 89.2 3.7 121.4 4.4 314.2 2.8 557.7 0.6 790.7 2.2 900.3 1.6 92.5 126.7 323.0 561.2 808.3 914.7 6 88.9 3.6 120.1 4.2 297.7 1.8 526.8 –0.8 789.1 0.4 905.2 0.8 92.2 125.1 303.1 522.8 792.4 912.2 8 88.7 3.5 118.9 3.9 285.1 0.9 508.3 –2.1 795.6 –1.1 916.1 –0.5 91.9 123.5 287.6 497.5 786.8 912.0 10 88.6 3.4 117.9 3.5 275.6 –0.1 497.9 –3.5 815.9 –3.7 932.5 –2.3 91.6 122.0 275.4 480.5 786.0 910.8 12 88.5 3.1 117.2 3.0 268.4 –1.0 492.6 –4.8 843.8 –6.9 953.9 –5.2 91.3 120.7 265.6 469.1 785.3 904.4 14 88.5 2.8 116.7 2.3 262.9 –2.0 490.5 –5.9 878.5 –11 966.3 –8.2 91.0 119.4 257.6 461.5 779.9 887.3 T/106N·m–1 第一带隙下限 第一带隙上限 第二带隙下限 第二带隙上限 第三带隙下限 第三带隙上限 FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% 0.5 74.3 3.4 89.3 2.8 259.2 0.7 440.3 –1.2 574.1 0.1 770.1 0.5 76.8 91.8 261.0 434.9 574.4 774.3 1.5 96.3 3.4 143.1 4.6 345.5 3.2 589.6 0.2 952.1 2.2 1035.1 1.7 99.6 149.7 356.7 591.0 973.0 1053.1 2.5 103.3 2.9 174.6 4.6 415.0 4.2 648.0 0.7 1217.4 2.8 1274.1 2.3 106.4 182.7 432.6 652.4 1251.0 1303.2 3.5 106.8 2.7 196.4 4.4 474.9 4.8 691.4 1.1 1434.1 3.0 1478.6 2.5 109.6 205.0 497.6 698.8 1477.6 1516.1 4.5 108.8 2.5 212.5 4.1 528.2 5.1 729.6 1.4 1621.6 3.2 1642.5 3.3 111.5 221.3 555.2 740.1 1673.4 1696.5 10 113.0 2.1 257.8 3.0 757.3 5.9 907.9 2.7 1645.9 5.8 1741.8 3.1 115.3 265.6 801.7 932.8 1740.6 1796.2 100 116.2 1.8 311.0 1.2 1654.1 5.2 1737.3 3.1 2270.8 9.0 2375.3 6.1 118.3 314.9 1740.4 1791.6 2475.7 2520.3 l1/mm 第一带隙下限 第一带隙上限 第二带隙下限 第二带隙上限 第三带隙下限 第三带隙上限 FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% 99 88.4 4.4 119.1 5.7 302.1 3.4 533.0 1.3 772.3 3.4 891.4 2.4 92.3 125.9 312.5 540.0 798.6 912.9 148 74.5 3.4 101.5 5.1 301.2 3.5 513.3 1.1 772.6 3.4 873.7 2.4 77.1 106.7 311.7 519.1 798.9 894.4 197 66.0 2.9 89.9 4.7 301.9 3.5 500.0 1.1 772.4 3.3 836.0 1.9 67.9 94.1 312.5 505.3 798.2 851.8 246 60.1 2.6 81.4 4.5 303.2 3.5 488.5 1.0 697.6 1.2 734.1 0.9 61.7 85.1 313.7 493.3 705.9 740.6 295 55.8 2.5 75.0 4.3 304.7 3.4 475.7 0.9 587.8 0.7 637.5 0.7 57.2 78.2 315.2 479.9 591.9 642.3 344 52.5 2.4 69.8 4.2 306.3 3.4 458.4 0.7 507.5 0.6 558.9 3.1 53.7 72.7 316.6 461.5 510.8 576.4 V2/10–4m3 第一带隙下限 第一带隙上限 第二带隙下限 第二带隙上限 第三带隙下限 第三带隙上限 FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% FEM
TMM误差/% 7.07 108.5 6.3 120.5 5.8 406.9 1.0 566.2 1.0 809.9 1.9 953.1 1.2 115.3 127.6 411.0 571.8 825.3 964.2 10.57 103.3 4.8 121.1 4.8 361.4 1.6 558.3 –0.1 796.5 1.9 925.4 1.4 108.3 126.8 367.2 557.8 811.4 938.7 14.07 98.0 4.2 121.0 4.4 335.0 1.9 550.0 –0.1 790.9 1.8 913.1 1.4 102.2 126.4 341.3 549.4 804.9 925.8 17.57 93.3 3.9 120.9 4.3 317.7 2.1 544.4 –0.1 788.3 1.6 906.5 1.3 96.9 126.1 324.4 543.9 801.1 918.1 19.32 91.1 3.8 120.8 4.3 311.1 2.2 542.3 –0.1 787.4 1.6 904.1 1.2 94.5 126.0 317.9 541.8 799.7 915.3 -
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]
计量
- 文章访问数:7750
- PDF下载量:138
- 被引次数:0













 下载:
下载: