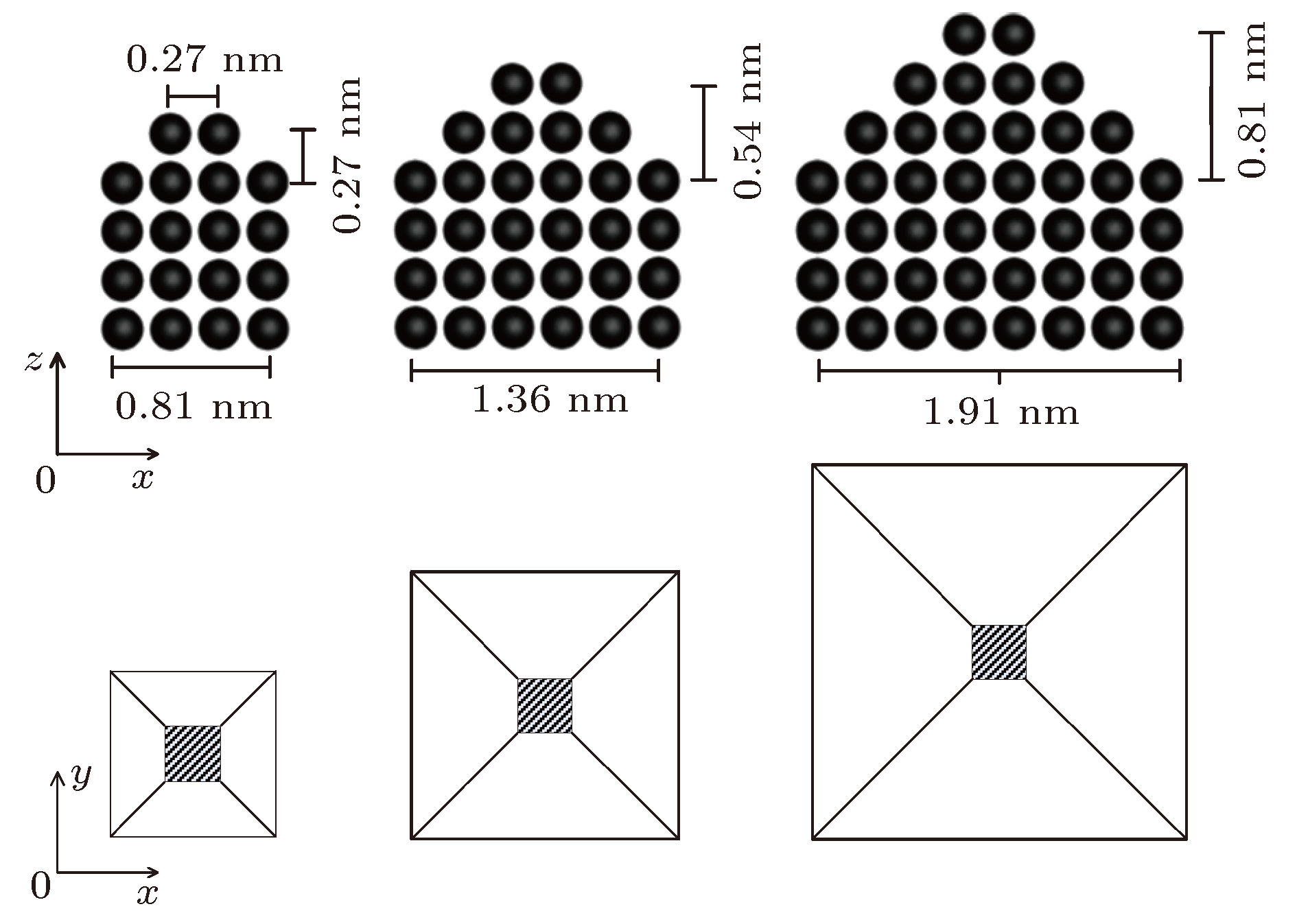
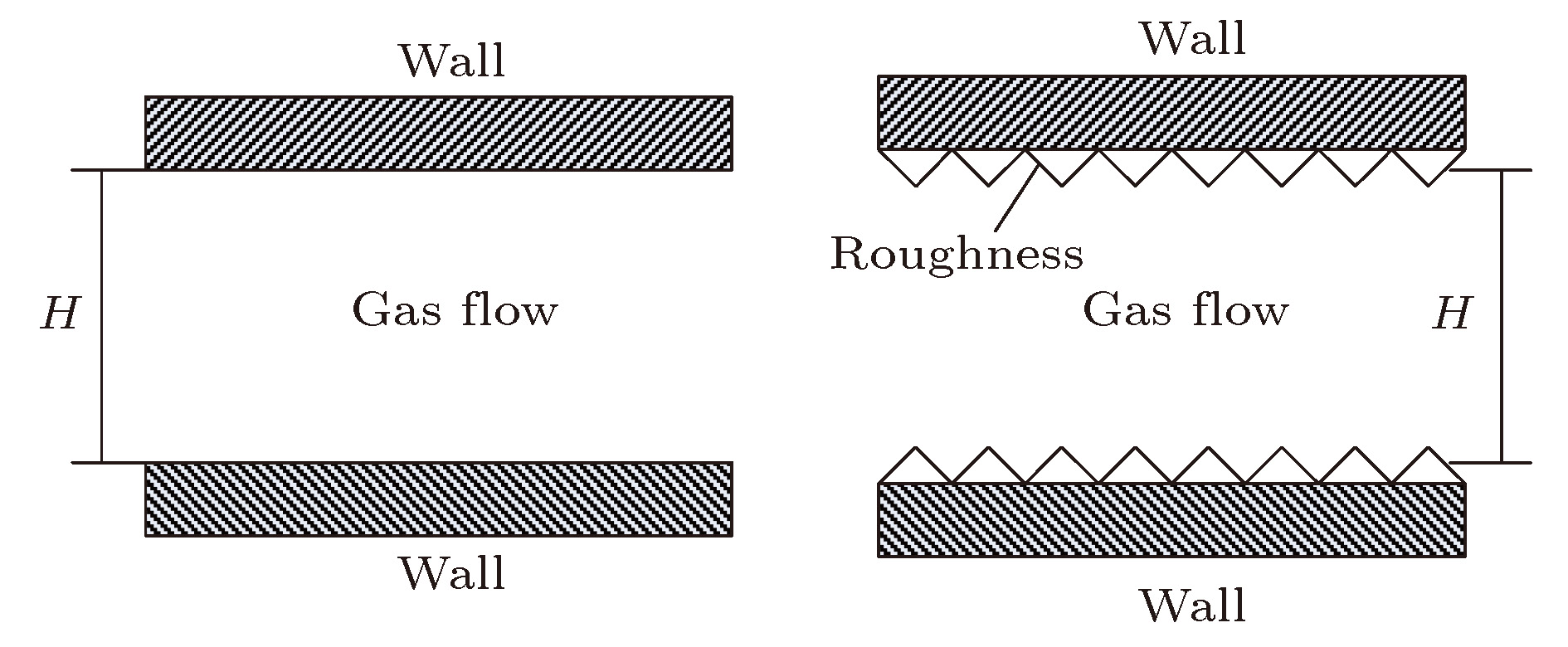
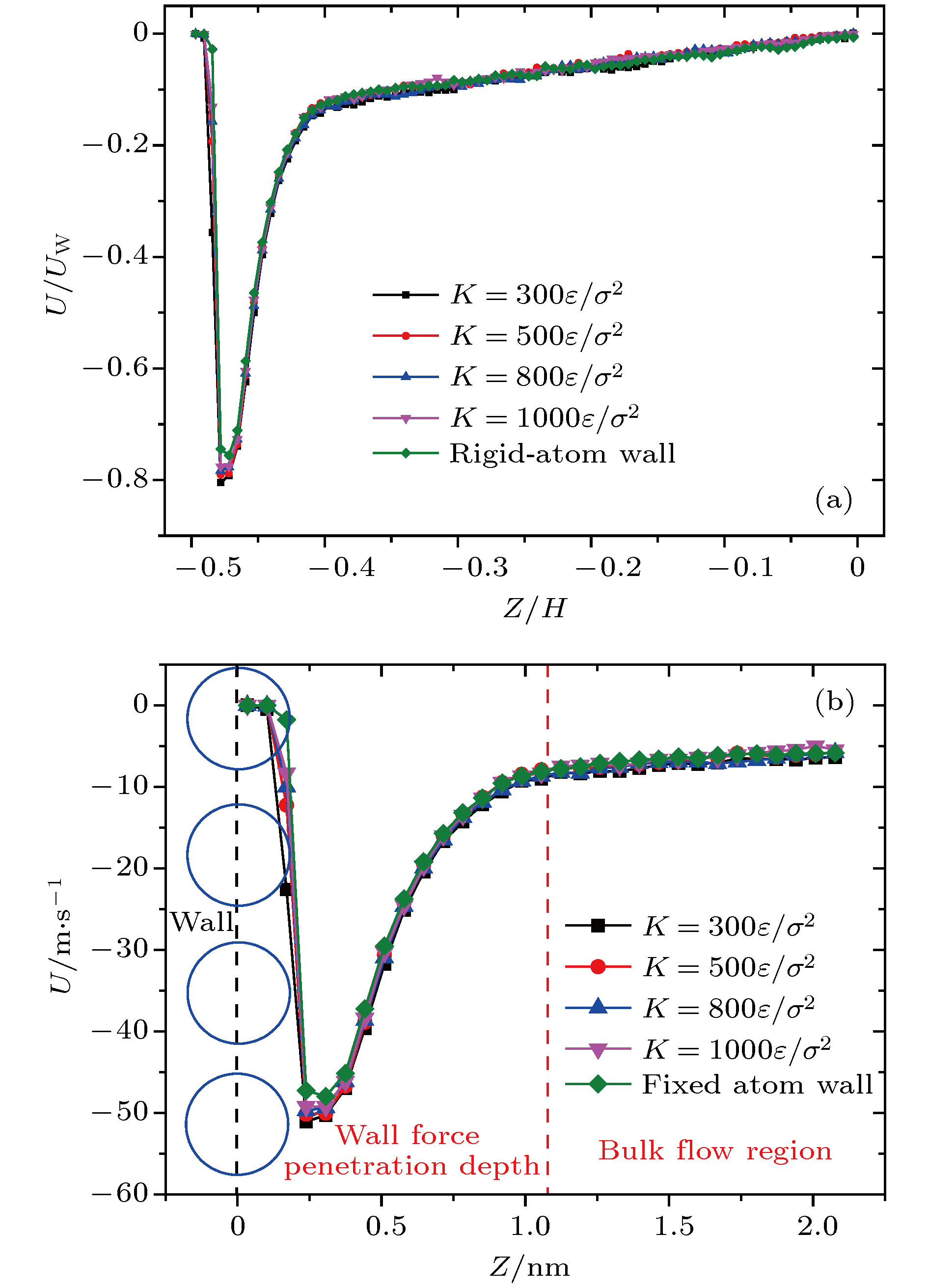
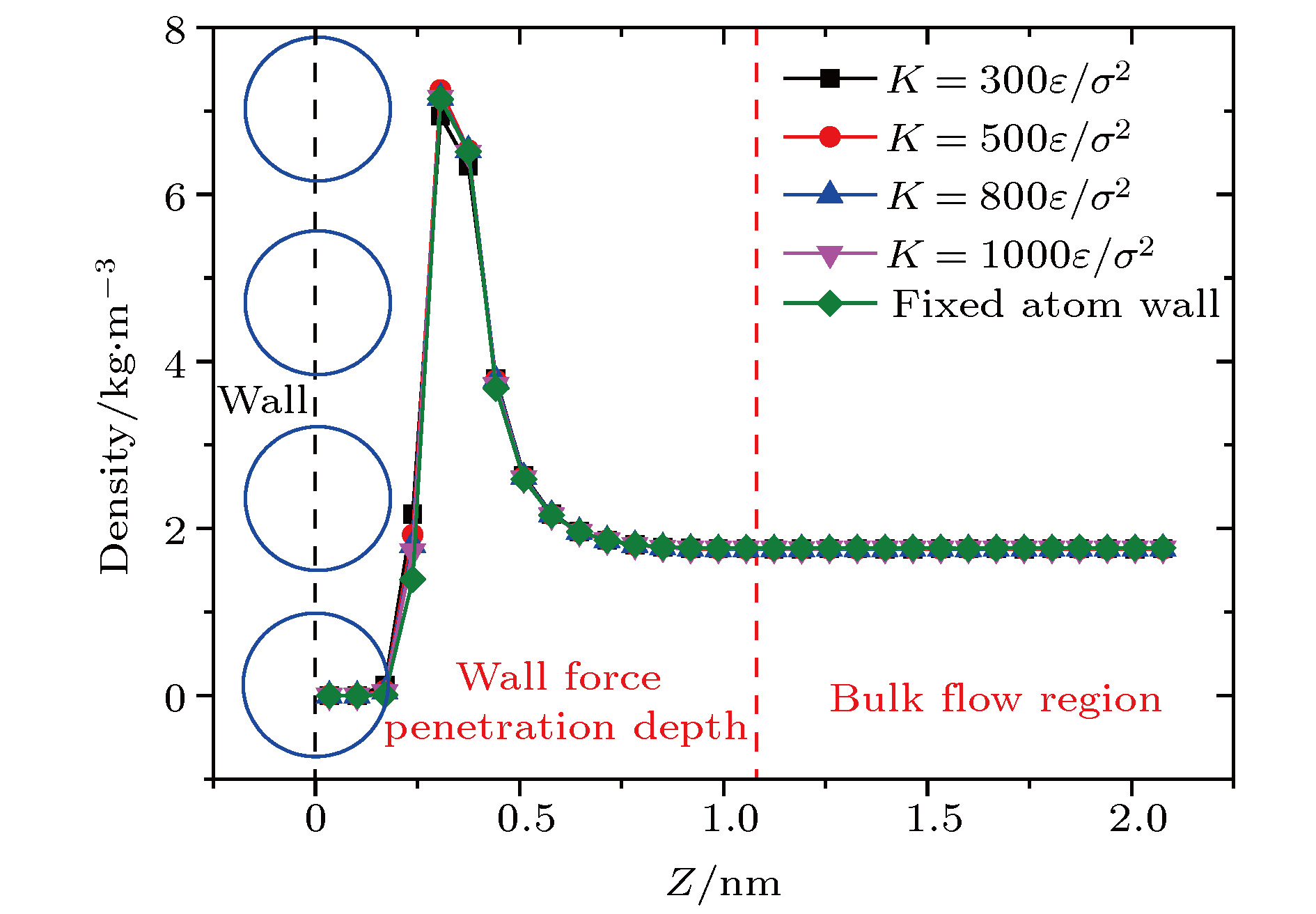
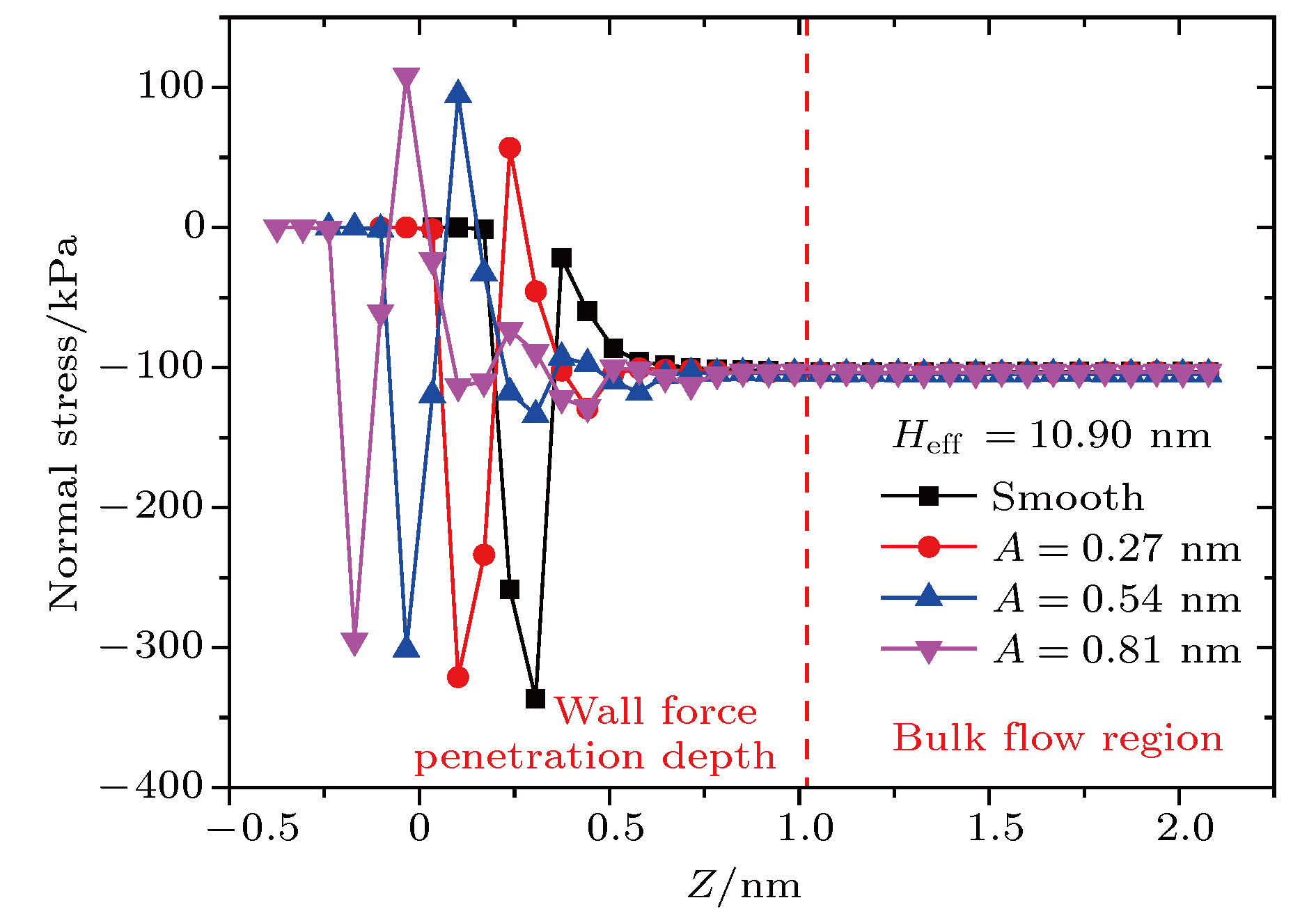
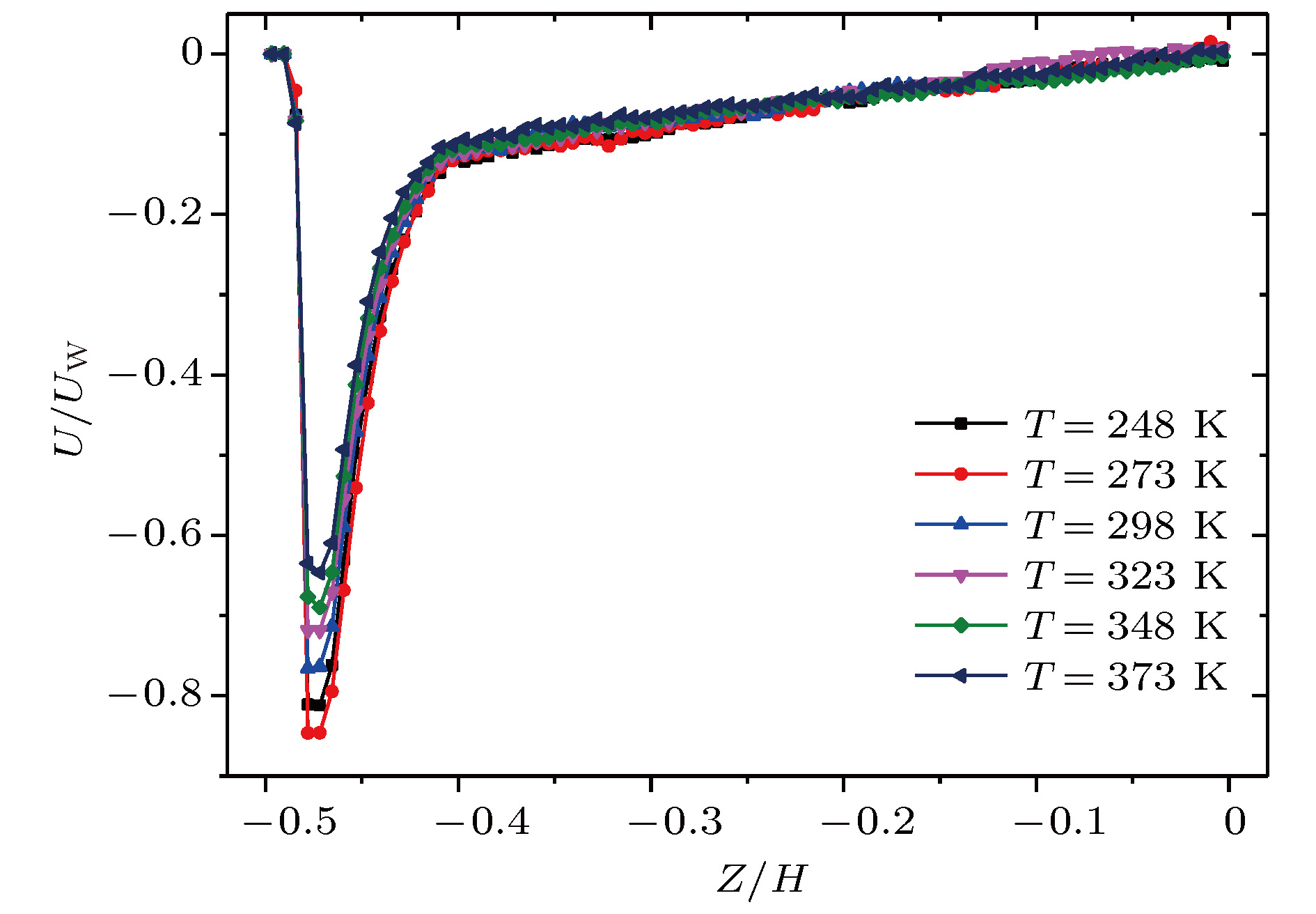
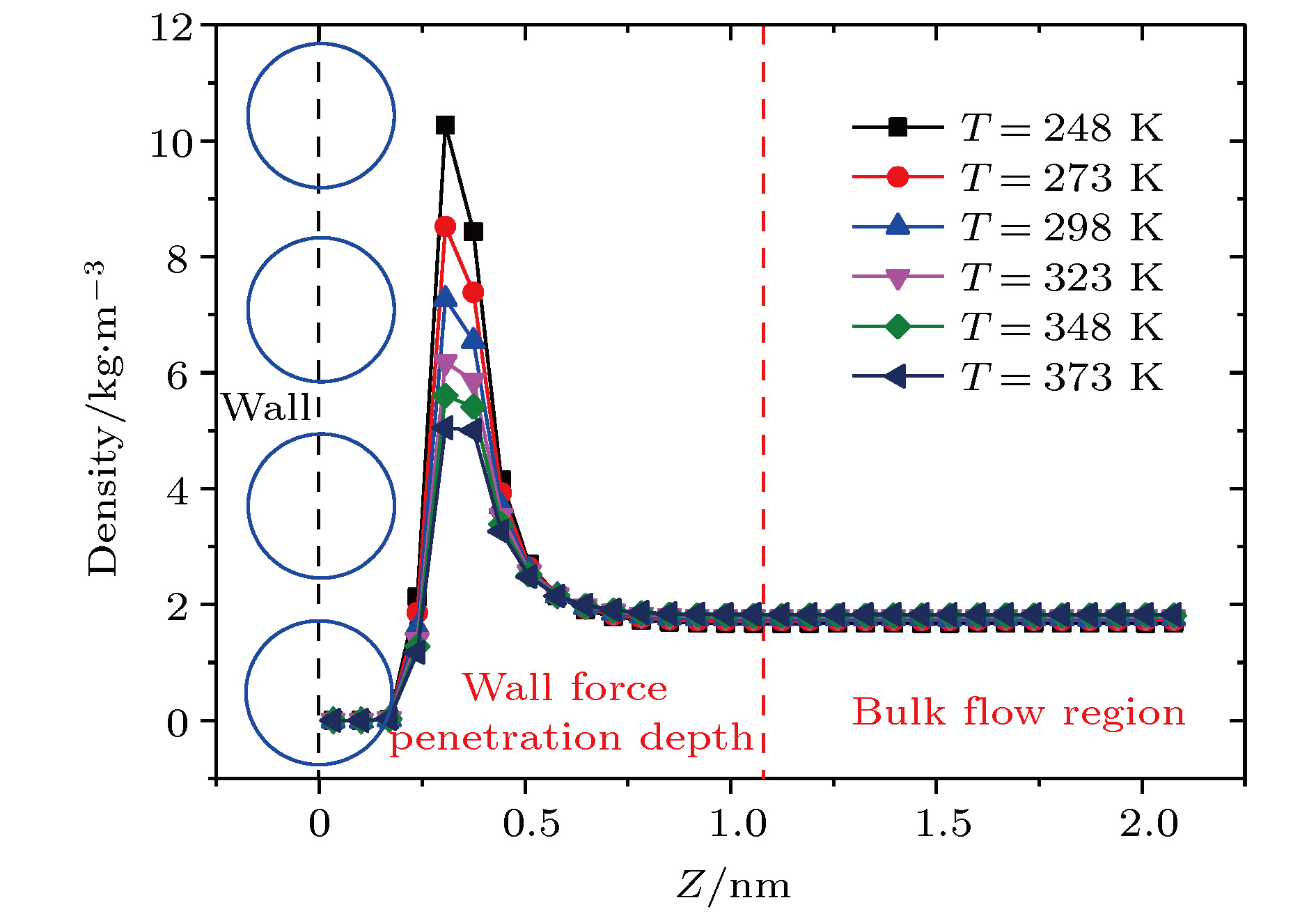
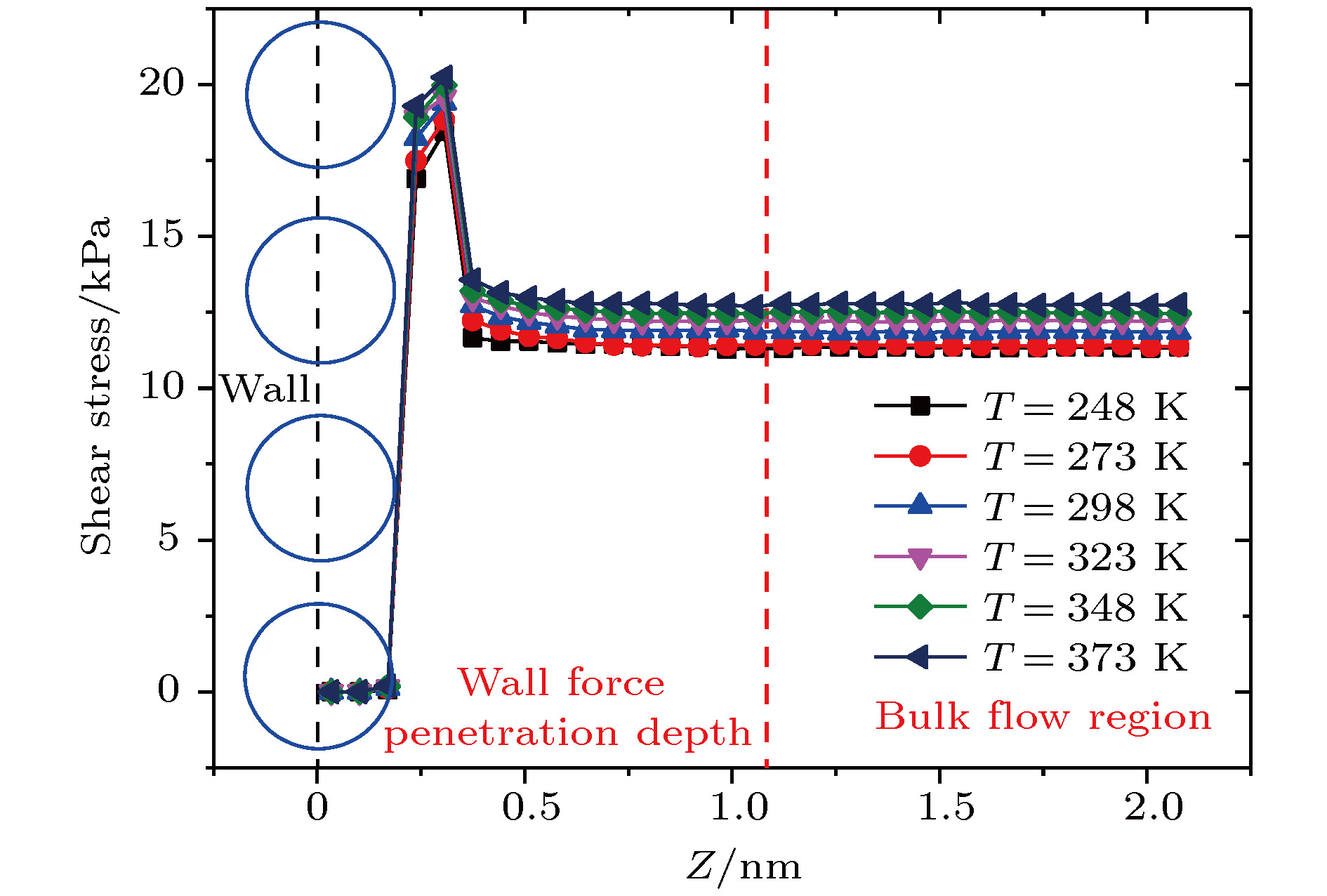
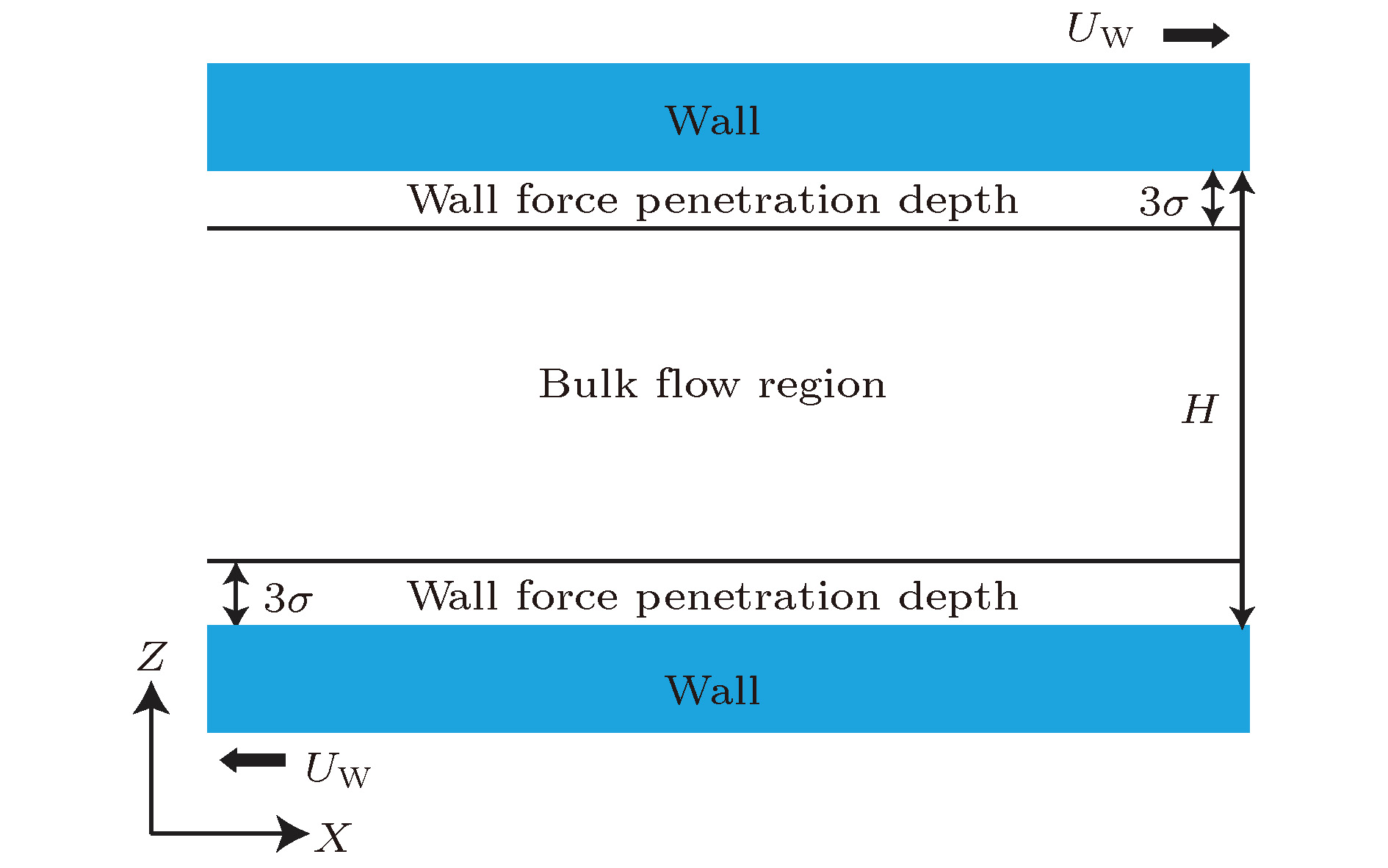
A three-dimensional non-equilibrium molecular dynamics method is adopted to investigate the influence of wall force field on the nanoscale gas flow in the transition regime. For the gas flow under nanoscale condition, the dominant effect of the wall force field on the flow field is more obvious, and the flow physical quantity is more sensitive to the change of the wall condition and system temperature. The motion of the wall atoms is governed by the Einstein theory, with using an elastic coefficient
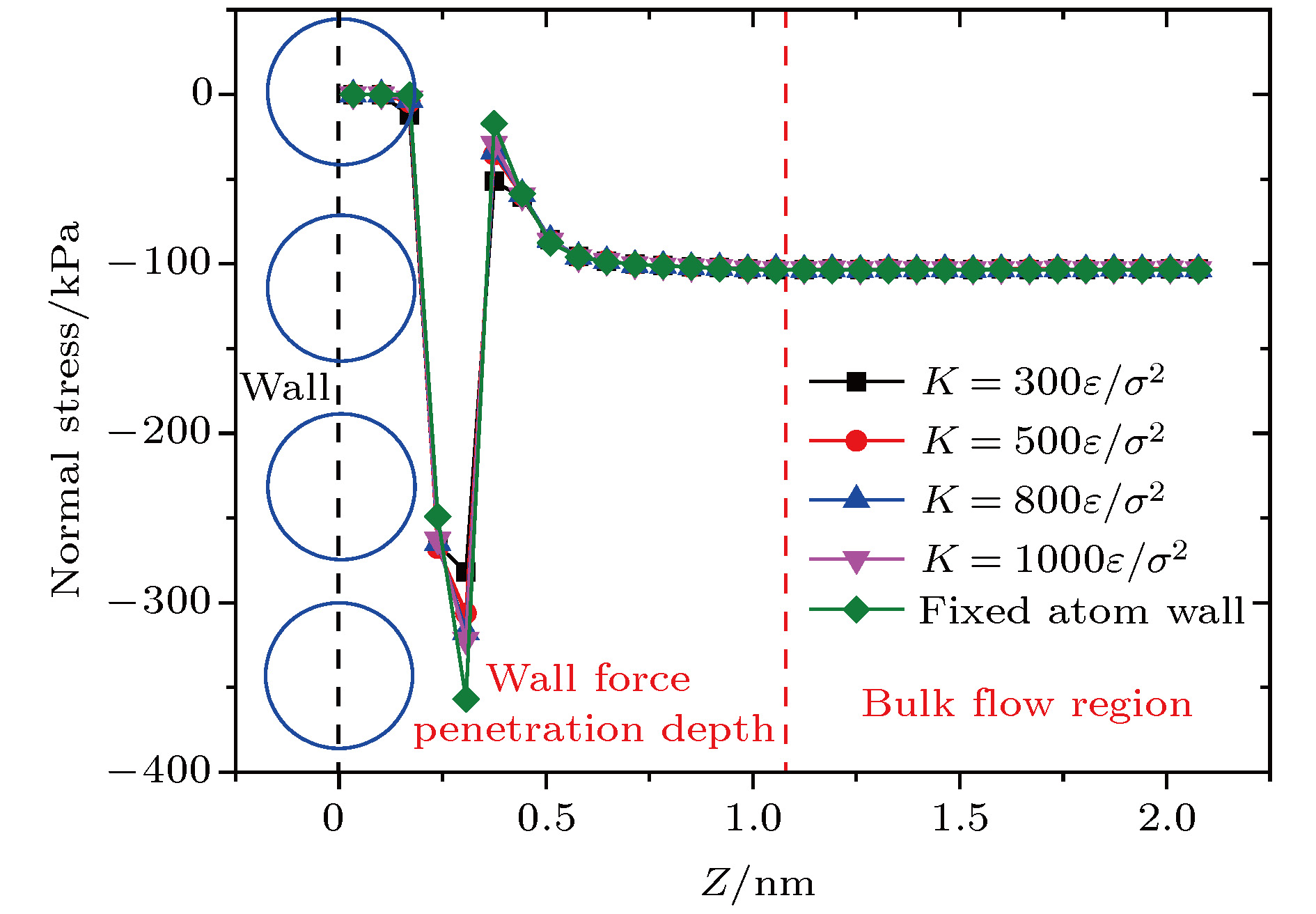
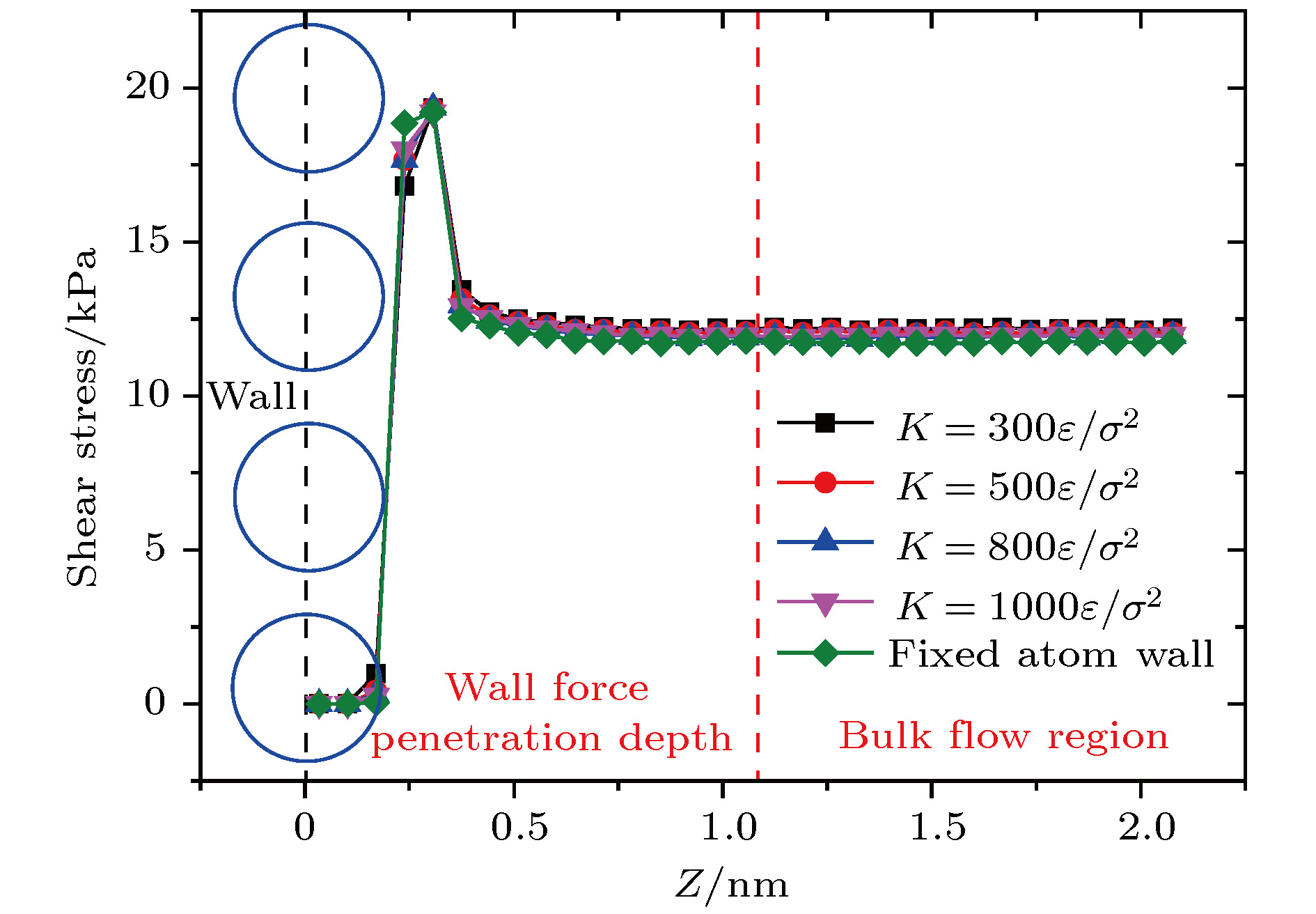
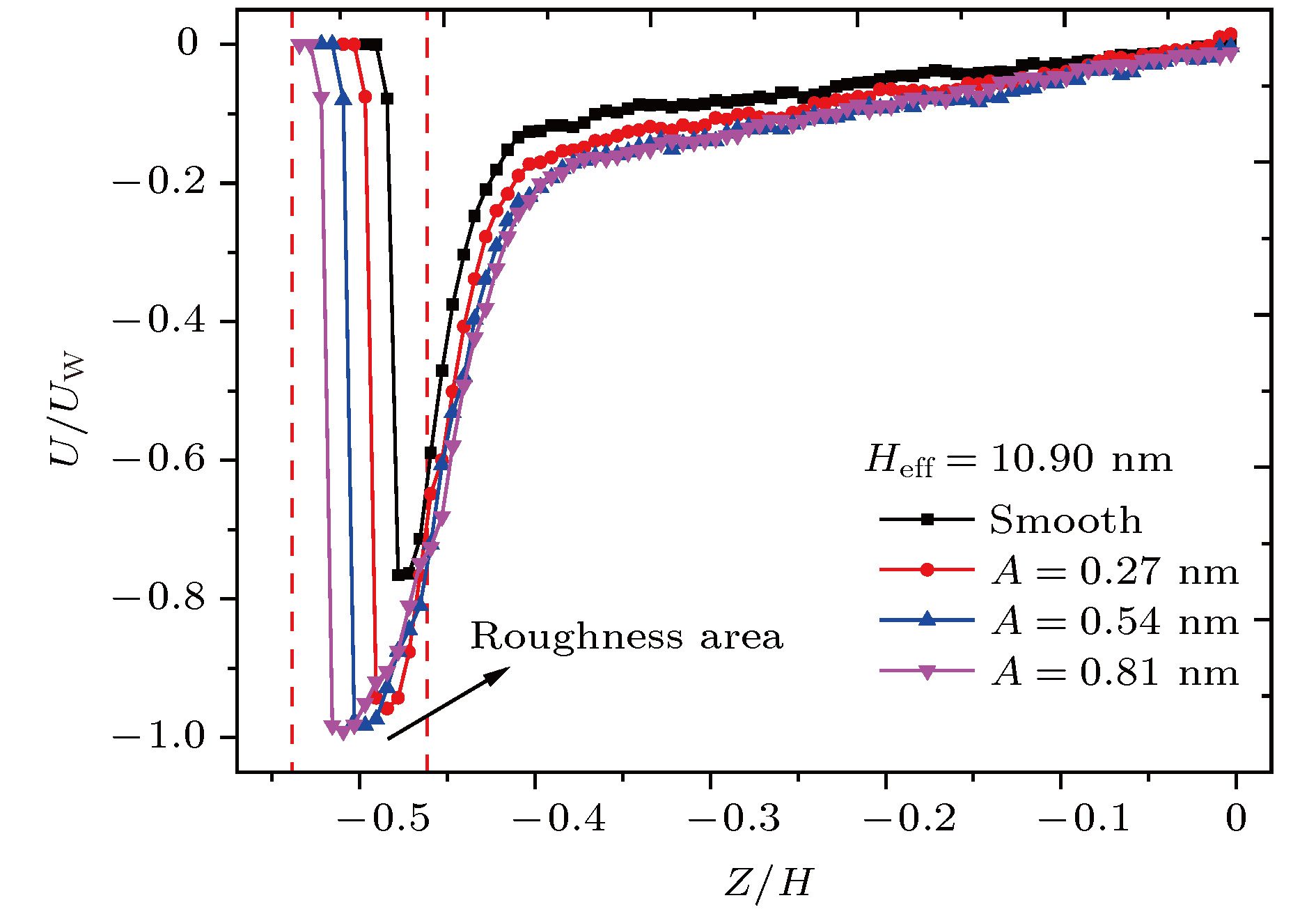
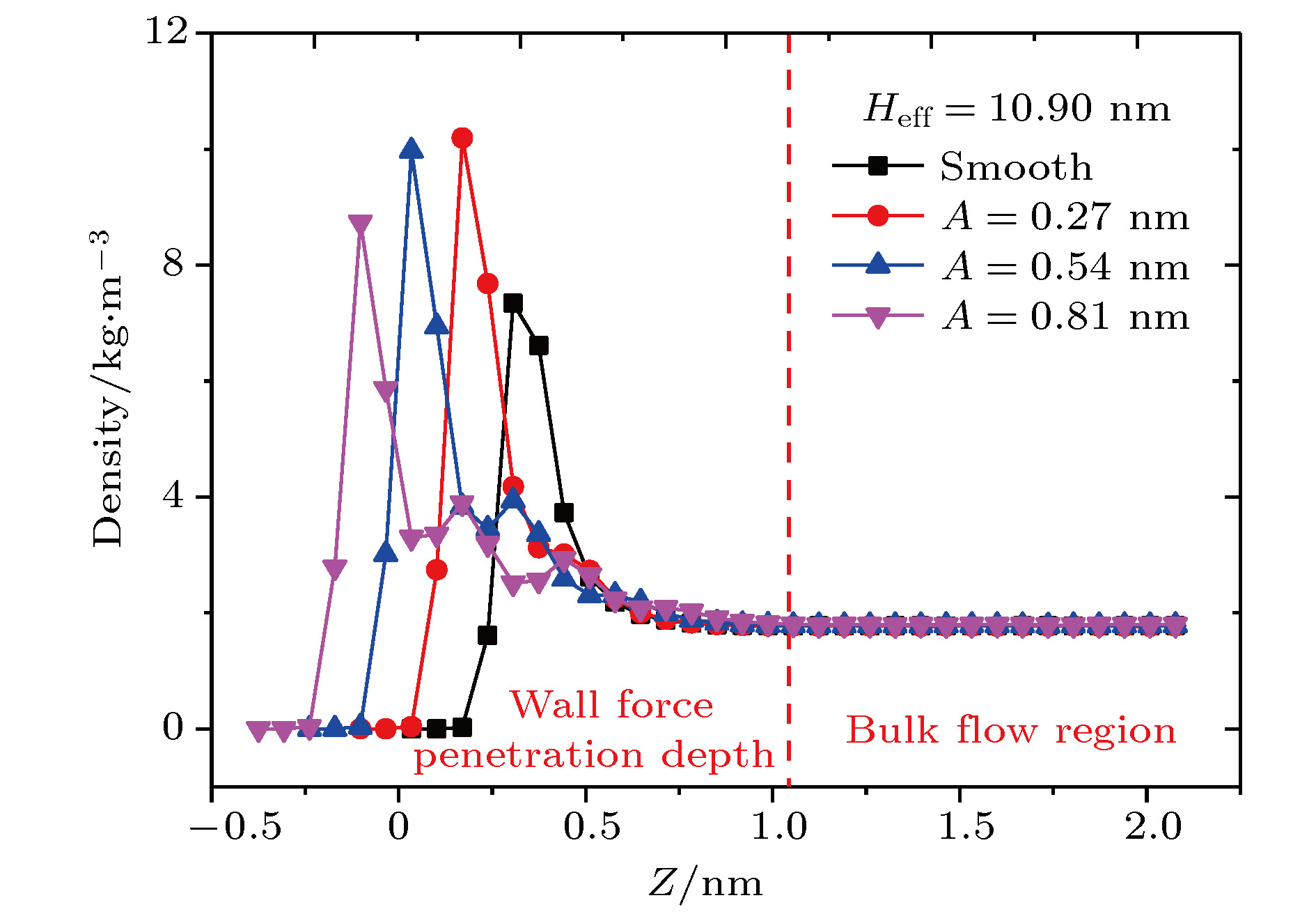
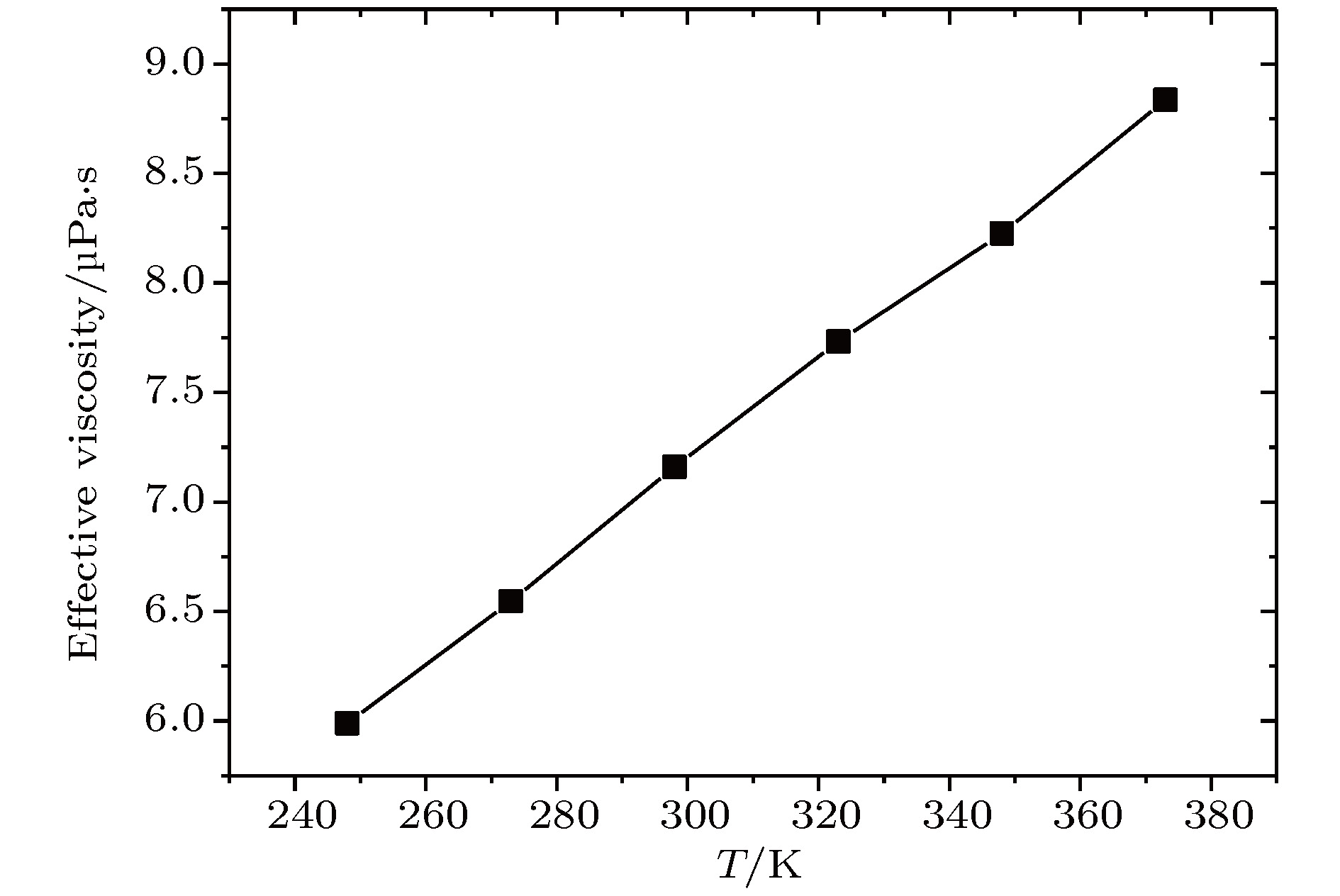
kto model the surface stiffness. The results indicate that the surface stiffness has little effect on the physical quantity distribution of the bulk flow region, but a certain influence on that of the near wall region. Increasing the value of the stiffness changes the velocity peak of the gas in the near-wall region and the tangential momentum adaptation coefficient (TMAC) towards lower values, thus demoting the momentum adaptability of the gas molecules to the surface. The wall roughness is simulated by a typical pyramidal model. It is found that the influence of wall roughness on the flow is very obvious, whether it is in the bulk flow region or in the near wall region. For the former case, the increase of roughness leads gas velocity and shear stress to increase, with density and normal stress remaining constant. The linear distribution of physical quantities is also affected to some extent. While for the latter case, as the roughness increases, the velocity of the fluid increases rapidly and approaches to the wall velocity. The peak of density increases, and the adsorption of gas molecules at the surface is obvious. The TMAC approaches to 1, suggesting that the gas and the surface achieve a complete momentum adaptation. Besides, the influence of system temperature on the gas flow in the nanochannel is also studied. The system temperature is controlled by the Nose-Hoover thermostat, making the flow field maintained at the target temperature through the damping coefficient. The results show that the effect of temperature is global in the whole flow region. The increase of temperature causes the flow velocity of the whole flow field to decrease, while the normal stress and shear stress to increase. A higher temperature leads to more frequent collisions between gas molecules, thus increasing the effective viscosity of the gas. At the same time, the degree of gas molecule adsorption in the near-wall region is reduced, contributing to a smaller TMAC value, and consequently a weaker gas-surface interaction.













 下载:
下载: