-
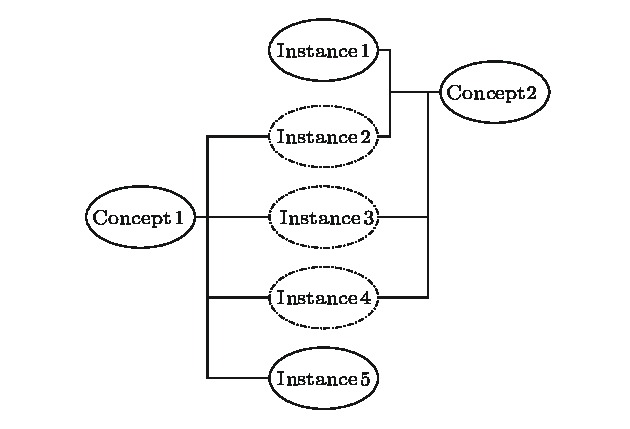
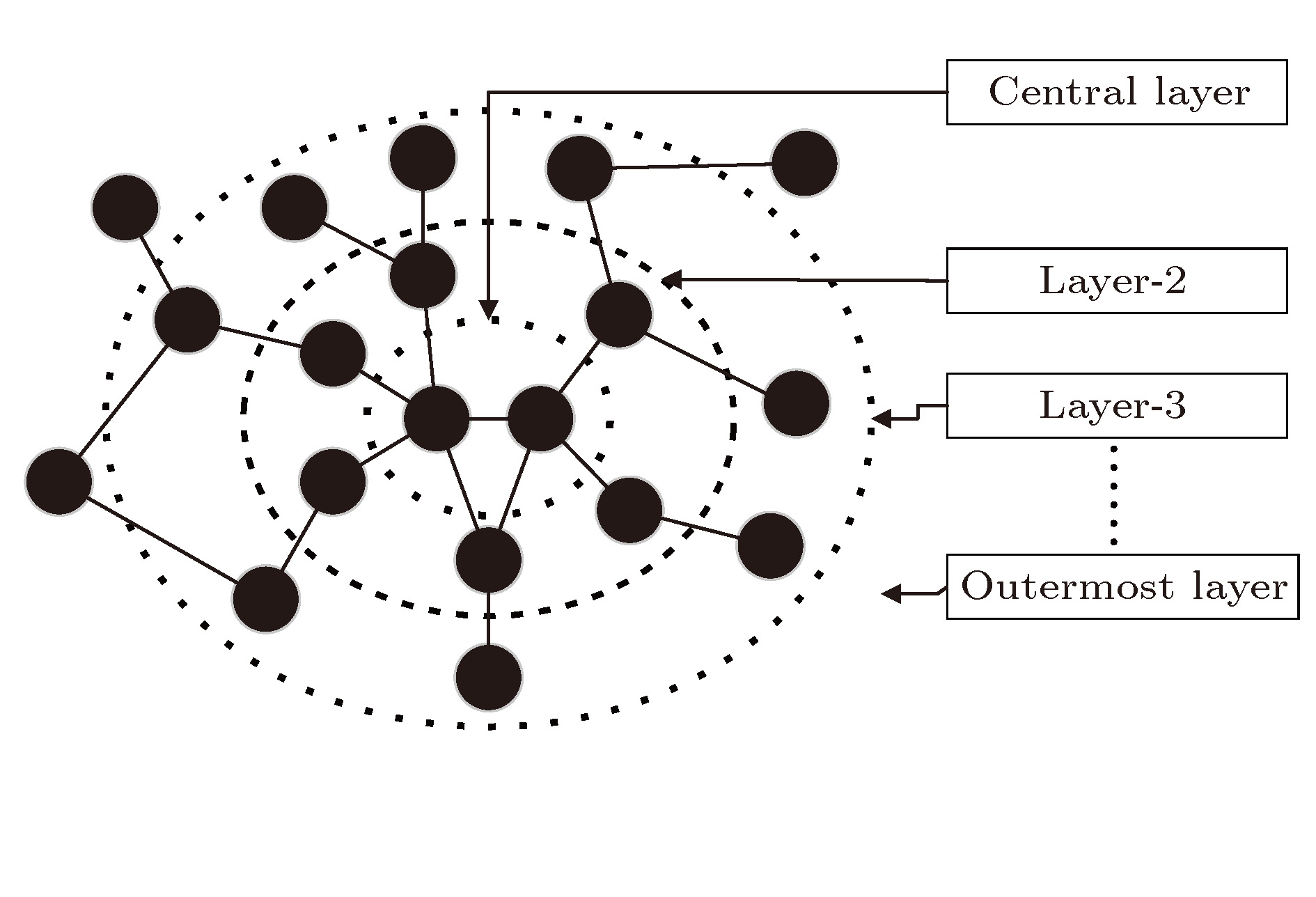
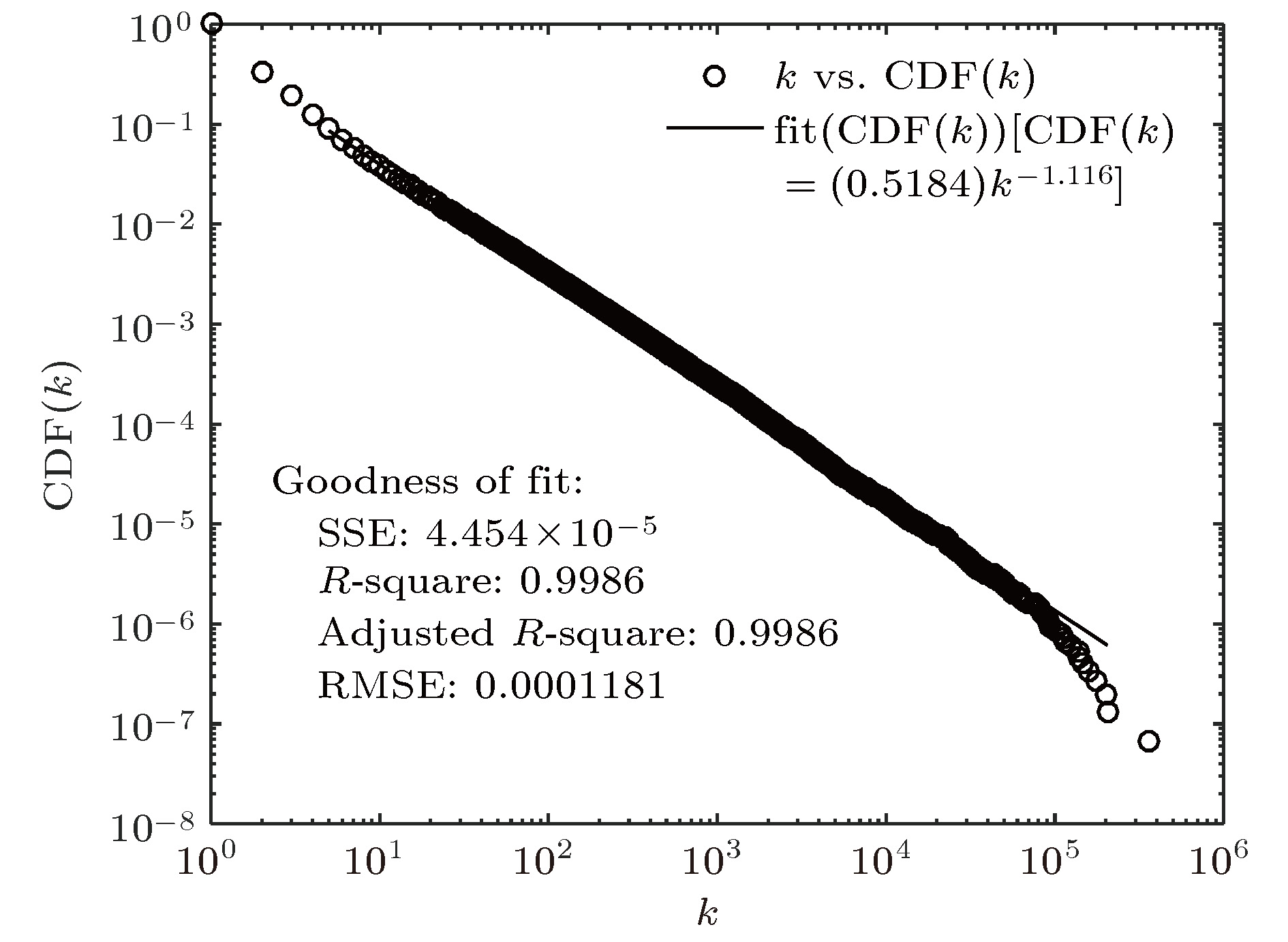
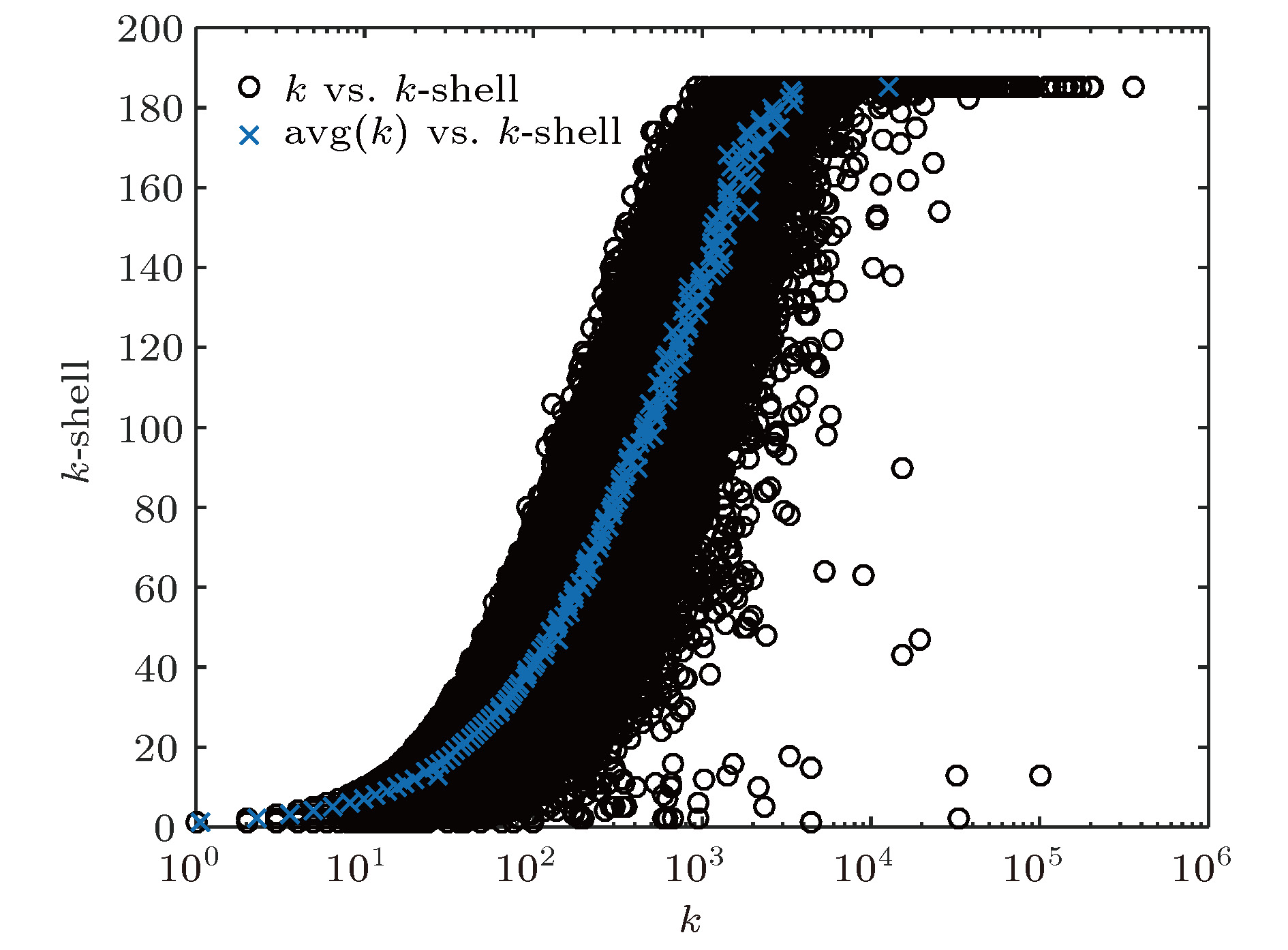
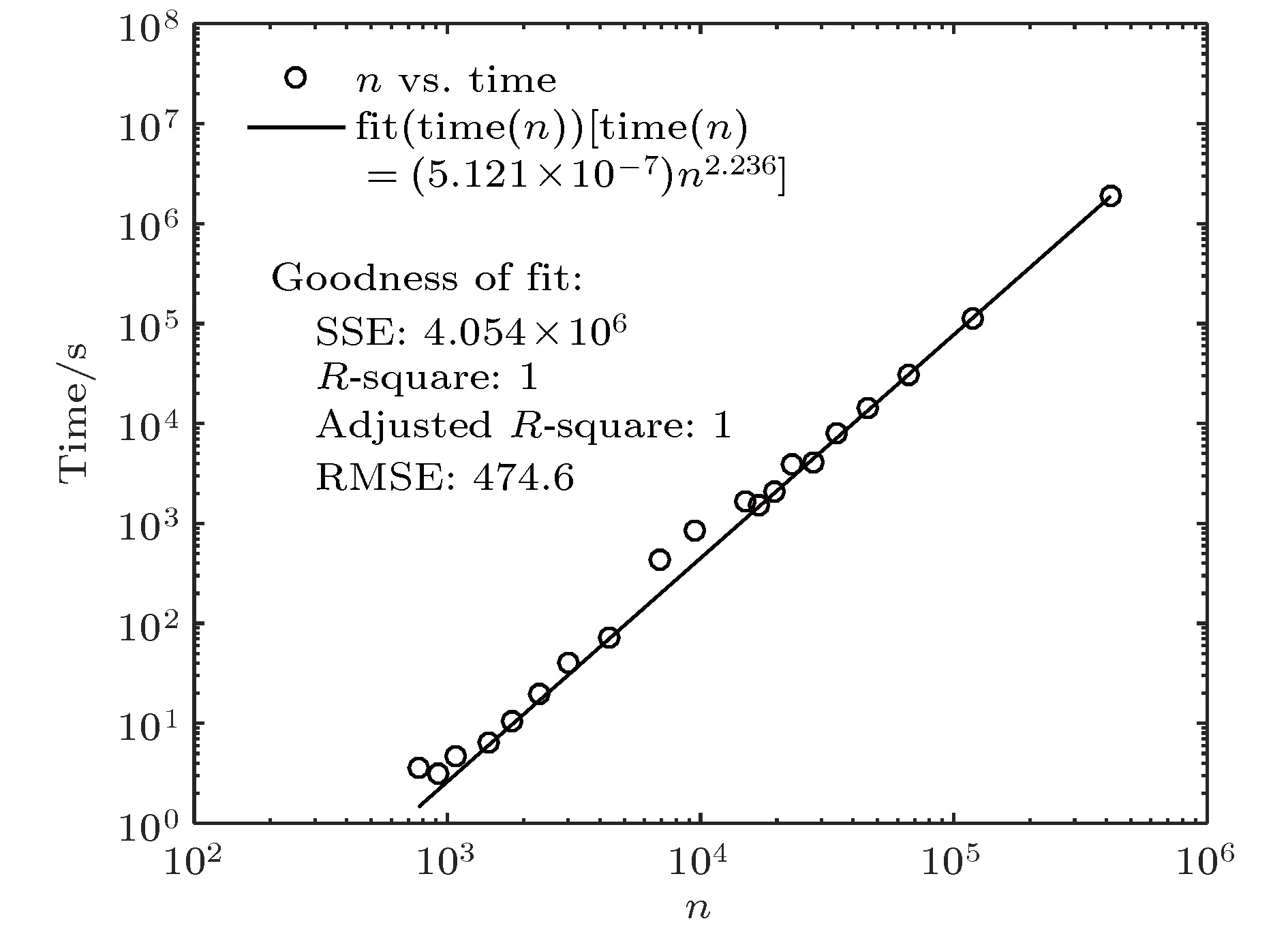
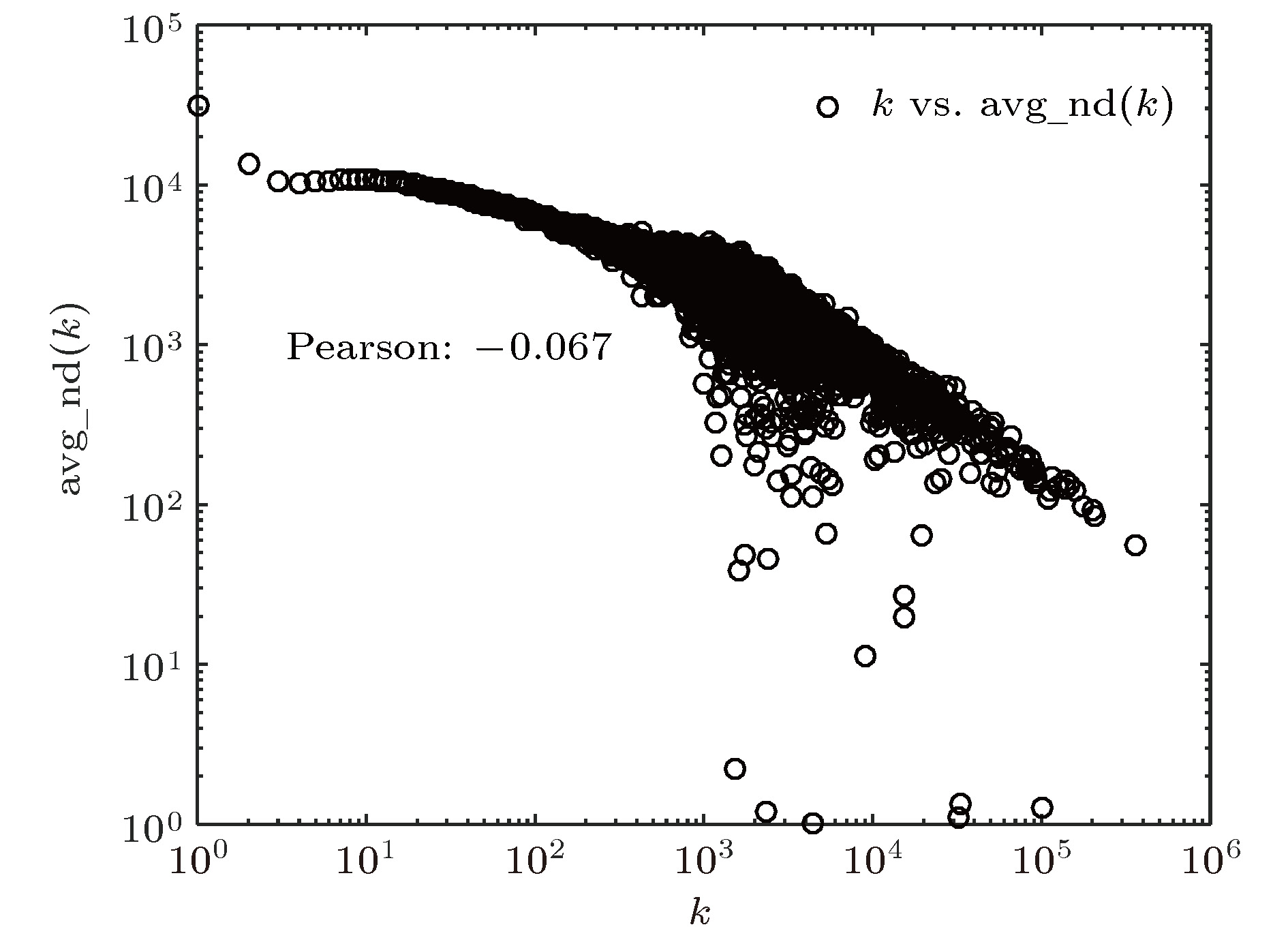
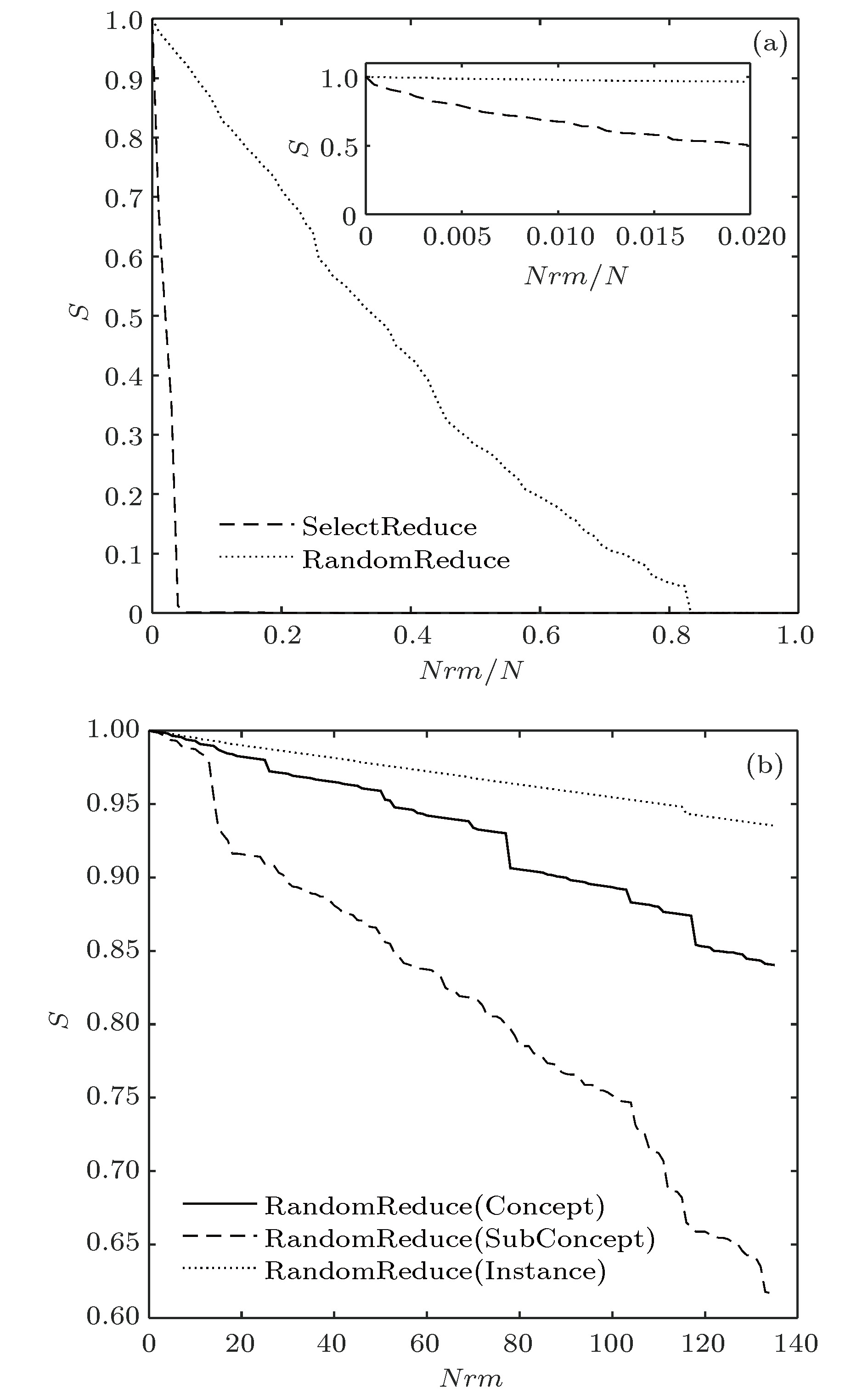
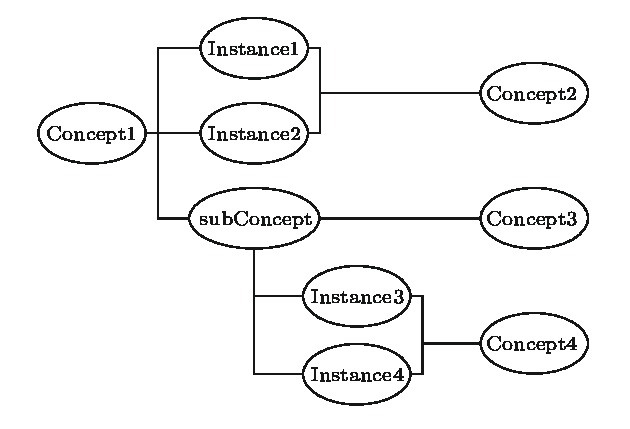
知识图谱是人工智能研究的新热点, 用于解决智能检索、自动回答等应用问题. 概念图谱是微软发布的大型知识图谱, 本文以概念图谱为研究对象构建了概念图谱网络, 并对其特性进行了分析. 为解决概念图谱海量数据带来的计算困难, 提出一种适合概念图谱的最大子网构建方法和一种网络近似平均路径的计算方法; 对不同度值给出了不同的聚类系数求解方法, 并通过Map/Reduce模式进行提速. 结果表明: 概念图谱网络具有无标度和极端小世界网络的特征; 平均路径长度随网络规模增加而减小并趋于4这一定值, 网络的“菱形”结构能很好地解释这一现象; 概念图谱网络是异构的, 相邻节点的度负相关; k-shell分解表明子概念占核心层节点的99.5%, 在概念图谱中起重要的连接作用; 子概念的缺失对概念图谱的完整性影响最大、概念其次、实例最小; 82%的实例节点度为1, 40%的概念节点度为1, 实例比概念更不易因一词多义而引起理解歧义.Knowledge graph is a hot topic in artificial intelligence area and has been widely adopted in intelligent search and question-and-answer system. Knowledge graph can be regarded as a complex network system and analyzed by complex network theory, which studies the interaction or relationship between various factors and basic characteristics of complex system. Its characteristics and their physical meanings are very helpful in understanding the nature of the knowledge graph. Concept graph is a large-scaled knowledge graph published by Microsoft. In this paper, we construct a huge complex network according to Microsoft’s concept graph. Its complex network characteristics, such as degree distribution, average shortest distance, clustering coefficient and degree correlation, are calculated and analyzed. The concept graph is not a connected network and its scale is very large; an approach is proposed to extract its largest connected subnet. The method has obvious advantages in both time complexity and space complexity. In this paper, we also present a method of calculating the approximate average shortest path of the largest connected subnet. The method estimates the maximum and minimum value of the shortest distance between nodes according to the distance between the central node and the network layer that the node belongs to and the distance between different layers. In order to calculate the clustering coefficient, different methods are introduced for nodes with different degree values and Map/Reduce idea is adopted to reduce the time cost. The experimental results show that the largest subnet of the concept graph is an ultra-small world network with the characteristics of scale-free. The average shortest path length decreases towards 4 with the network size increasing, which can be easily explained by the diamond-shaped network structure. The concept graph is a disassortative network where low degree nodes tend to connect to high degree nodes. The subConcepts account for 99.5% of nodes in the innermost k-core after k-shell decomposition. It shows that the subConcepts play an important role in the connectivity of network. The absence of subConcept affects the complexness of concept graph most, the concept next, and the instance least. The 82% instance nodes and 40% concept nodes of the concept graph each have a degree value of 1. It is believed that compared with the concept words, the instance words do not lead to the ambiguity in the understanding of natural language, caused by polysemy.
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] -
k Concept k Instance k SubConcept Quantity Proportion Quantity Proportion Quantity Proportion 1 2061496 0.464809 1 9610146 0.831317 1 18 1.91208 × 10–5 2 1165725 0.262838 2 1014355 0.087746 2 140735 0.149498132 3 538652 0.121451 3 312310 0.027016 3 186330 0.197932191 4 252438 0.056918 4 156703 0.013555 4 125273 0.133073361 5 130975 0.029531 5 96100 0.008313 5 78365 0.083244546 6 74760 0.016856 6 64809 0.005606 6 52113 0.055357915 7 46336 0.010447 7 46409 0.004015 7 37615 0.039957169 8 31509 0.007104 8 34801 0.00301 8 29314 0.031139292 9 22506 0.005074 9 27177 0.002351 9 23419 0.024877229 10 16510 0.003723 10 21928 0.001897 10 19484 0.020697208 11 12921 0.002913 11 18095 0.001565 11 16465 0.017490224 12 10012 0.002257 12 14935 0.001292 12 14188 0.015071443 13 8188 0.001846 13 12688 0.001098 13 12491 0.013268776 $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ 32773 1 2.25 × 10–7 6716 1 8.65 × 10–8 364276 1 1.06227 × 10–6 Total 4435143 1 Total 11560144 1 Total 941383 1 Algorithm Parameters Time complexity Time cost NetworkX — — — 15 d以上 SNEBF m= 15 114 834 n= 33 377 320 m× 2n= 15 114 834 × 2n 约5.22 a SNESO nl= 12 n= 33 377 320 nl× 3.2n= 19.2 × 2n 3.49 min (实际运算3.80 min) Algorithm Parameters Space complexity Memory cost NetworkX — — 40 GB ESNSO SubNeti, NeighborsSet, MaxSubNet 31724479 5.23 GB k Concept Instance SubConcept Total Quantity Percentage Quantity Percentage Quantity Percentage Quantity 1 1468308 40.3 8636049 82.0 0 0.0 10104357 2 1014641 27.9 968156 9.2 138875 14.8 2121672 3 503109 13.8 309716 2.9 185665 19.8 998490 4 242308 6.7 156248 1.5 125045 13.3 523601 5 127833 3.5 96027 0.9 78311 8.3 302171 6 73429 2.0 64778 0.6 52090 5.6 190297 7 45834 1.3 46398 0.4 37604 4.0 129836 8 31237 0.9 34799 0.3 29301 3.1 95337 9 22401 0.6 27173 0.3 23417 2.5 72991 10 16439 0.5 21925 0.2 19488 2.1 57852 11 12880 0.4 18095 0.2 16464 1.8 47439 12 9981 0.3 14934 0.1 14187 1.5 39102 13 8169 0.2 12688 0.1 12503 1.3 33360 $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ Total 3639631 ··· 10536663 ··· 938540 ··· 15114838 node k node k factor 364343 Event 113364 feature 204130 company 110609 issue 202331 program 93963 product 174283 technique 92341 item 159164 application 90644 area 144595 organization 90605 topic 137781 Name 87637 service 137398 Case 85863 activity 124670 method 84157 information 114500 project 82122 t n e t n e t n e t n e 10 415491 936536 60 27654 66704 150 9492 19845 600 1788 2637 20 119367 303323 70 23089 54533 200 6850 13315 700 1453 2059 30 66272 169774 80 19567 45510 300 4336 7566 800 1076 1487 40 45410 114629 90 17042 38921 400 3013 4920 900 922 1222 50 34467 85085 100 15086 33983 500 2318 3577 1000 770 994 Layer Quantity Layer Quantity Layer Quantity Layer Quantity 1 2 4 4639826 7 11921 10 73 2 553406 5 639119 8 1609 11 16 3 9202185 6 66347 9 327 12 3 Layer t= 10 t= 20 t= 30 t= 50 t= 100 t= 200 t= 300 t= 500 t= 1000 1 2 2 2 2 2 2 2 2 2 2 26993 10212 6226 3409 1534 748 456 258 88 3 223659 65471 34244 16456 6445 2437 1305 558 103 4 131967 36095 21646 12077 5712 2829 1722 832 205 5 28219 6590 3563 2037 1116 656 661 438 108 6 3745 821 505 418 206 129 157 187 128 7 766 143 74 55 62 41 30 29 89 8 98 25 12 11 7 4 3 13 29 9 27 6 — 2 2 3 — 1 13 10 12 2 — — — 1 — — 5 11 3 — — — — — — — — k Nk knn(k) k Nk knn(k) 1 10104357 31235.02 159164 1(item) 122.577 2 2121672 13384.27 174283 1(product) 98.812 3 998490 10435.94 202331 1(issue) 91.266 4 523601 10231.12 204130 1(feature) 85.926 5 302171 10388.98 364343 1(factor) 56.088 $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$ -
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35]
计量
- 文章访问数:10202
- PDF下载量:153
- 被引次数:0













 下载:
下载: