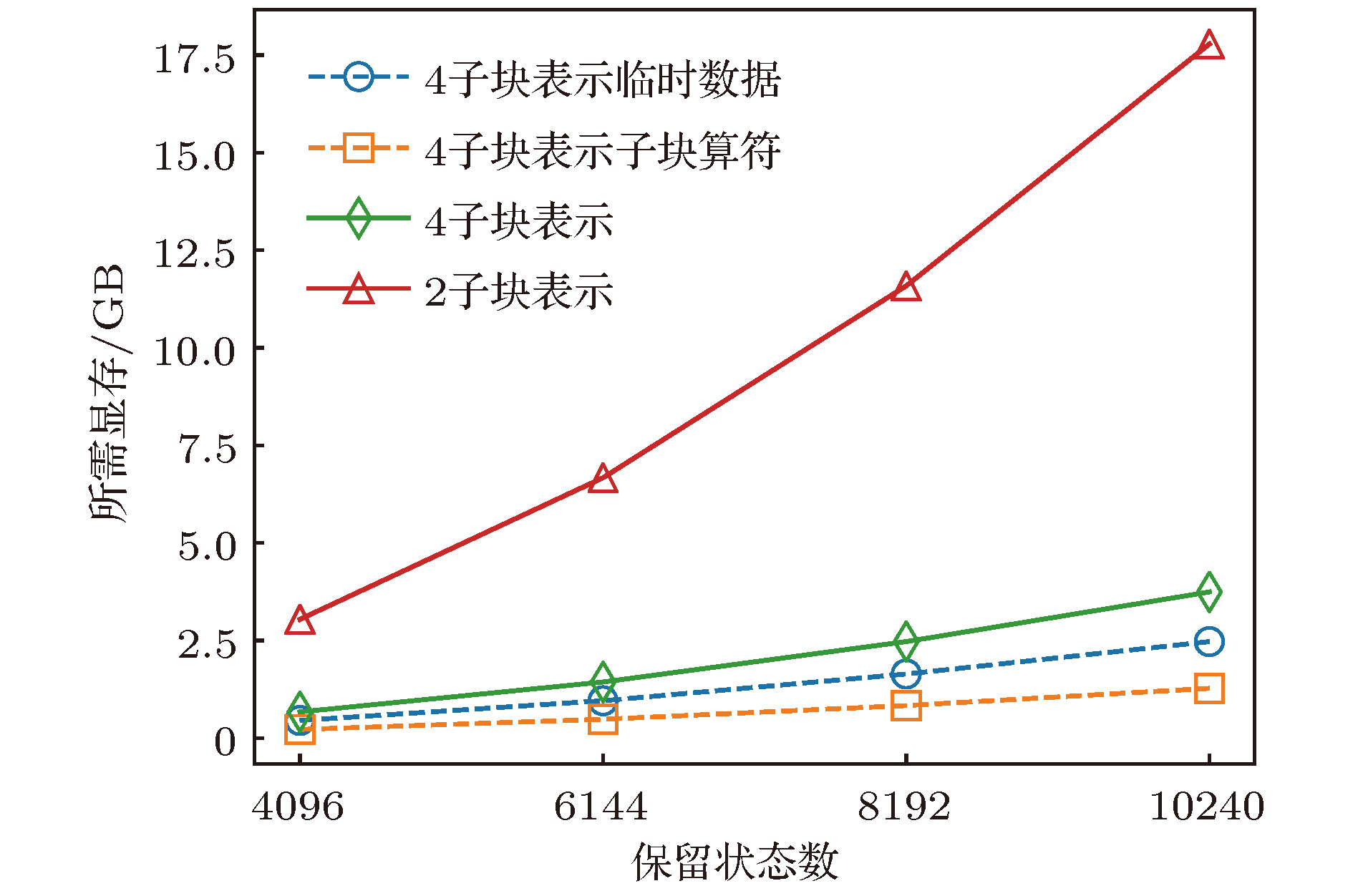
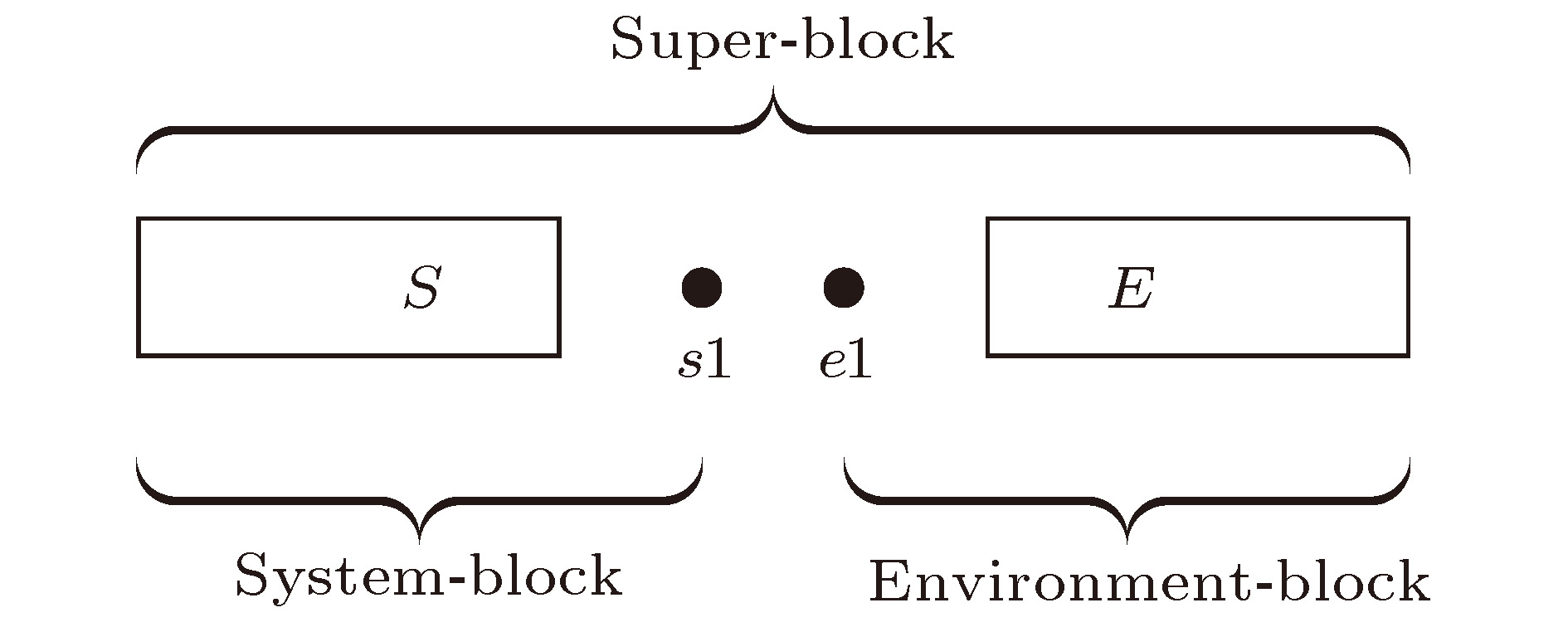
Density matrix renormalization group (DMRG), as a numerical method of solving the ground state of one-dimensional strongly-correlated lattice model with very high accuracy, requires expensive computational and memory cost when applied to two- and quasi-two-dimensional problems. The number of DMRG kept states is generally very large to achieve a reliable accuracy for these applications, which results in numerous matrix and vector operations and unbearably consuming time in the absence of the proper parallelization. However, due to its sequential nature, the parallelization of DMRG algorithm is usually not straightforward. In this work, we propose a new hybrid parallelization strategy for the DMRG method. It takes advantage of the computing capability of both central processing unit (CPU) and graphics processing unit (GPU) of the computer. In order to achieve as many as DMRG kept states within a limited GPU memory, we adopt the four-block formulation of the Hamiltonian rather than the two-block formulation. The later consumes much more memories, which has been used in another pioneer work on the hybrid parallelization of the DMRG algorithm, and only a small number of DMRG kept states are available. Our parallel strategy focuses on the diagonalization of the Hamiltonian, which is the most time-consuming part of the whole DMRG procedure. A hybrid parallelization strategy of diagonalization method is implemented, in which the required data for diagonalization are distributed on both the host and GPU memory, and the data exchange between them is negligible in our data partitioning scheme. The matrix operations are also shared on both CPU and GPU when the Hamiltonian acts on a wave function, while the distribution of these operations is determined by a load balancing strategy. Taking fermionic Hubbard model for example, we examine the running performance of the hybrid parallelization strategy with different DMRG kept states and provide corresponding performance benchmark. 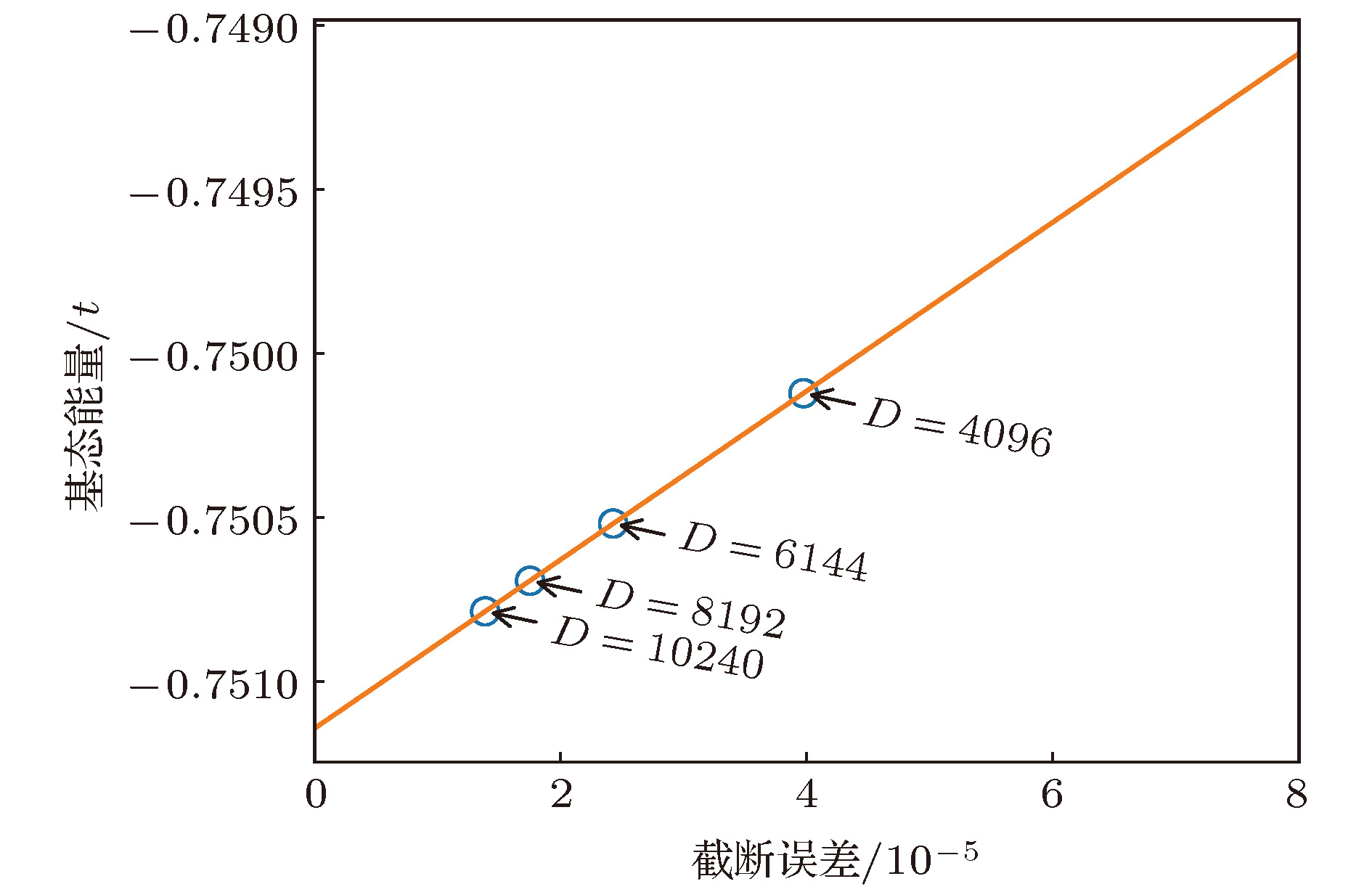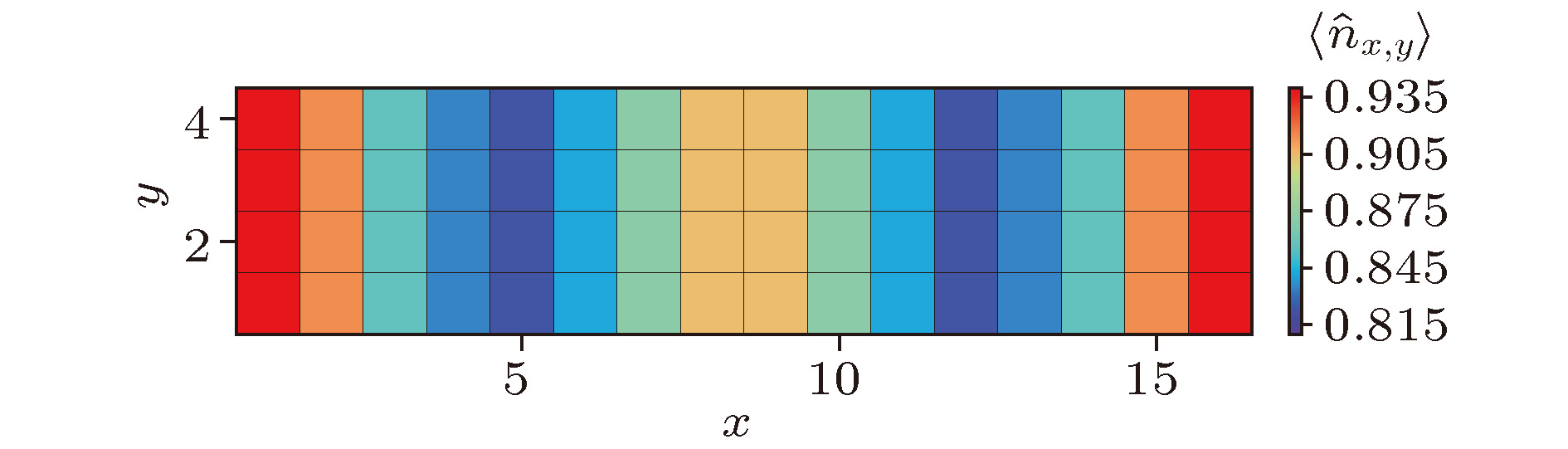On a 4-leg ladder, we employ the conserved quantities with U(1) symmetry of the model and a good-quantum number based task scheduling to further reduce the GPU memory cost. We manage to obtain a moderate speedup of the hybrid parallelization for a wide range of DMRG kept states. In our example, the ground state energy with high accuracy is obtained by the extrapolation of the results, with different numbers of states kept, and we show charge stripes which are usually experimentally observed in high-temperature superconductors. In this case, we keep 10 ⁴DMRG states and the GPU memory cost is less than 12 Gigabytes.